
(2011山东烟台,26,14分)
如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=-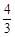 x+
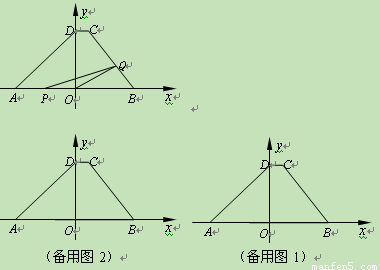
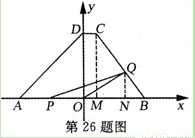
x+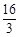 ,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运行.动点Q自点B出发,在折线BCD上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ的面积为s(不能构成△OPQ的动点除外).
(1)求出点B、C的坐标;
(2)求s随t变化的函数关系式;
(3)当t为何值时s有最大值?并求出最大值.


(1)把y=4代入y=- x+
x+ ,得x=1.
,得x=1.
∴C点的坐标为(1,4).
当y=0时,- x+
x+ =0,
=0,
∴x=4.∴点B坐标为(4,0).
(2)作CM⊥AB于M,则CM=4,BM=3.
∴BC= =
= =5.
=5.
∴sin∠ABC=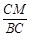 =
=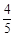 .
.
①当0<t<4时,作QN⊥OB于N,
则QN=BQ·sin∠ABC=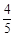 t.
t.
∴S=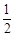 OP·QN=
OP·QN=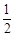 (4-t)×
(4-t)×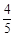 t =-
t =- t2+
t2+ t(0<t<4).
t(0<t<4).
②当4<t≤5时,(如备用图1),
连接QO,QP,作QN⊥OB于N.
同理可得QN=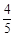 t.
t.
∴S=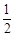 OP·QN=
OP·QN=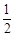 ×(t-4)×
×(t-4)×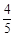 t.
t.
= t2-
t2- t(4<t≤5).
t(4<t≤5).
③当5<t≤6时,(如备用图2),
连接QO,QP.
S=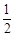 ×OP×OD=
×OP×OD=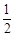 (t-4)×4.
(t-4)×4.
=2t-8(5<t≤6).
(3)①在0<t<4时,
当t= =2时,
=2时,
S最大= =
= .
.
②在4<t≤5时,对于抛物线S= t2-
t2- t,当t=-
t,当t=- =2时,
=2时,
S最小= ×22-
×22- ×2=-
×2=- .
.
∴抛物线S= t2-
t2- t的顶点为(2,-
t的顶点为(2,- ).
).
∴在4<t≤5时,S随t的增大而增大.
∴当t=5时,S最大= ×52-
×52- ×5=2.
×5=2.
③在5<t≤6时,
在S=2t-8中,∵2>0,∴S随t的增大而增大.
∴当t=6时,S最大=2×6-8=4.
∴综合三种情况,当t=6时,S取得最大值,最大值是4.
【解析】略


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源:2012学年人教版中考数学第一轮复习二元一次方程组专项训练 题型:选择题
(2011山东烟台,20,8分)小华从家里到学校的路是一段平路和一段下坡路.假设他始终保持平路每分钟走60米,下坡路每分钟走80米 ,上坡路每分钟走40米,从家里到学校需10分钟,从学校到家里需15分钟.请问小华家离学校多远?
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(北京卷)数学解析版 题型:解答题
(2011山东烟台,22,8分)
如图,已知反比例函数 (k1>0)与一次函数
(k1>0)与一次函数 相交于A、B两点,AC⊥x轴于点C.
若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C.
若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(北京卷)数学解析版 题型:解答题
(2011山东烟台,21,8分)
综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)

查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(北京卷)数学解析版 题型:选择题
(2011山东烟台,9,4分)如果△ABC中,sinA=cosB= ,则下列最确切的结论是(
)
,则下列最确切的结论是(
)
A. △ABC是直角三角形 B. △ABC是等腰三角形
C. △ABC是等腰直角三角形 D. △ABC是锐角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com