
【题目】如图,在平面直角坐标系中,△ABC内接于⊙P,AB是⊙P的直径,A(﹣1,0)C(3,2 ![]() ),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E.
),BC的延长线交y轴于点D,点F是y轴上的一动点,连接FC并延长交x轴于点E. 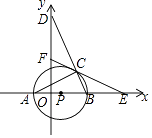
(1)求⊙P的半径;
(2)当∠A=∠DCF时,求证:CE是⊙P的切线.
【答案】
(1)解:作CG⊥x轴于G,
则AC2=AG2+CG2=(3+1)2+(2 ![]() )2=24,
)2=24,
由射影定理得:AC2=AGAB,
∴AB= ![]() =6,
=6,
∴⊙P的半径为3
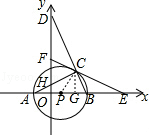
(2)解:证明:连接PC,
∵AB是⊙P的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵PC=PB,
∴∠PCB=∠PBC,
∵∠A=∠DCF=∠ECB,
∴∠ECB+∠PCB=90°,
∵C在⊙P上,
∴CE是⊙P的切线.
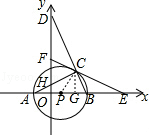
【解析】(1)作CG⊥x轴于G,根据勾股定理和射影定理即可得到结论;(2)连接PC,由AB是⊙P的直径,得到∠ACB=90°根据等腰三角形的性质得到∠PCB=∠PBC,根据切线的判定定理即可得到结论.
【考点精析】通过灵活运用三角形的外接圆与外心和切线的判定定理,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,过边AB上一点N作AB的垂线交BC于点M.
(1)如图1,若∠A=40°,求∠NMB的度数.
(2)如图2,若∠A=70°,求∠NMB的度数.
(3)你可以再分别给出几个∠A(∠A为锐角)的度数,你发现规律了吗?写出当∠A为锐角时,你猜想出的规律,并进行证明.
(4)当∠A为直角、钝角时,是否还有(3)中的结论(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴1<![]() <2.
<2.
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
(解决问题)![]() 的小数部分是多少;
的小数部分是多少;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求![]() 的近似值.
的近似值.
解:设![]() =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即![]() 的近似值为10.35.
的近似值为10.35.
理解应用:利用上面的方法求![]() 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的顶点A、B、D均在⊙O上,请仅用无刻度的直尺按要求作图.
(1)AB边经过圆心O,在图(1)中作一条与AD边平行的直径; 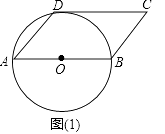
(2)AB边不经过圆心O,DC与⊙O相切于点D,在图(2)中作一条与AD边平行的弦. 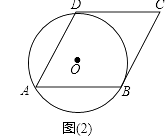
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以1.5m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示. 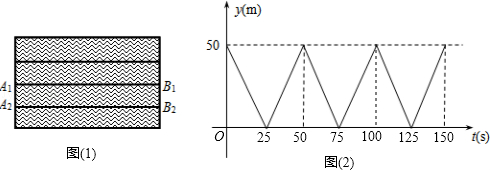
(1)赛道的长度是m,甲的速度是m/s;当t=s时,甲、乙两人第一次相遇,当t=s时,甲、乙两人第二次相遇?
(2)第三次相遇时,两人距池边B1B2多少米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
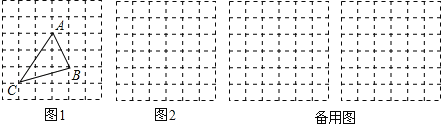
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.
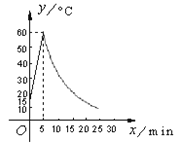
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. 
(1)线段AE=;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F. 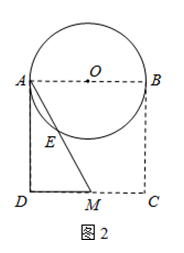
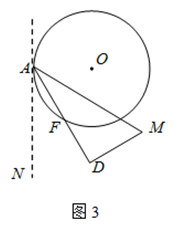
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ![]() 时,DM与⊙O相切.
时,DM与⊙O相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com