
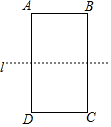
 如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.
如图,直线l是矩形ABCD的一条对称轴,AD=2AB,点P是直线l上一点,且使得△PAB和△PBC均为等腰三角形,则满足条件的点P共有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
分析 如图,设直线l交AD于P1,交BC于P2.只要证明四边形ABP2P1是正方形,可知△ABP1,△ABP2是等腰三角形,作AB的垂直平分线交直线l于P3,则△ABP3是等腰三角形,由此即可解决问题.
解答 解:如图,设直线l交AD于P1,交BC于P2.
∵四边形ABCD是矩形,直线l是对称轴,
∴四边形ABP2P1是正方形,
∵AD=2AB,
∴AP1=AP2,
∴四边形ABP2P1是正方形,
∴△ABP1,△ABP2是等腰三角形,
作AB的垂直平分线交直线l于P3,则△ABP3是等腰三角形,
∴满足条件的点P共有3个,
故选C
点评 本题考查矩形的判定和性质、等腰三角形的判定、正方形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
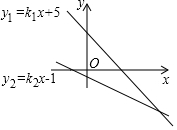 有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.
有两个一次函数:y1=k1x+5,y2=k2x-1.它们的图象交于点(5,-3),如图.那么,不等式(k1-k2)x<-6的解集是x>5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
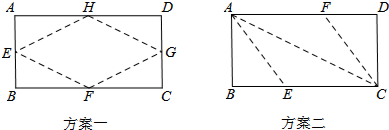
| A. | 方案一 | B. | 方案二 | ||
| C. | 两个方案一样 | D. | 无法通过计算来比较大小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
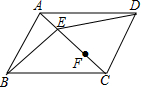 如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com