
����Ŀ�������Ѿ�ѧϰ������������y= ![]() ��ͼ������ʣ���ع��о����Ĺ��̣��Ժ���y=
��ͼ������ʣ���ع��о����Ĺ��̣��Ժ���y= ![]() ����̽�������н��ۣ�
����̽�������н��ۣ�
��ͼ���ڵ�һ�������ޣ���ͼ���ڵ�һ�������ޣ�
��ͼ�����y��Գƣ���ͼ�����ԭ��Գƣ�
�ݵ�x��0ʱ��y��x���������x��0ʱ��y��x���������
��x��0ʱ��y��x�������С����x��0ʱ��y��x���������
�Ǻ���y= ![]() �����ʼ�����ͼ���������ǣ� �� ����д������ȷ�𰸵���ţ�
�����ʼ�����ͼ���������ǣ� �� ����д������ȷ�𰸵���ţ�
���𰸡��٢ۢ�
���������⣺�б���
x | ��3 | ��2 | ��1 |
| 1 | 2 | 3 |
y |
|
| 1 | 4 | 1 |
|
|
��ͼ��
�ɺ���y= ![]() ��ͼ���֪��ͼ������������ʣ�
��ͼ���֪��ͼ������������ʣ�
������ͼ����һ�������ޣ���x��0ʱ��y��x�������С����x��0ʱ��y��x�������������ͼ�����y�Գƣ�
��ѡ�٢ۢޣ�
�����㾫����������Ĺؼ��������ⷴ�������������ʵ����֪ʶ����������:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ������������Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABE=��ACD=Rt����AE=AD����ABC=��ACB.��֤����BAE=��CAD��
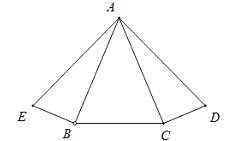
�벹ȫ֤�����̣�����������д�����ɣ�
֤��������ABC�У�
�ߡ�ABC=��ACB
��AB= �� ��
��Rt��ABE��Rt��ACD��
�� =AC�� =AD
��Rt��ABE��Rt��ACD�� ��
���BAE=��CAD�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�A������Ϊ��2��4����B������Ϊ����3����2����C������Ϊ��3��1����
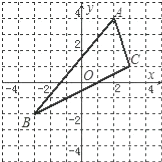
��1����ͼ�л�����ABC����y��ԳƵġ�A��B��C�䣨��д����������д����A�䣬B�䣬C������ꣻ
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�ڡ�ABC�У���C=30�㣬���ǰѡ�A�ĶԱ����C �ĶԱߵıȽ�����A�����ң�����thi A����thi A= ![]() =
= ![]() �������������⣺ ��֪���ڡ�ABC�У���C=30�㣮
�������������⣺ ��֪���ڡ�ABC�У���C=30�㣮
��1������A=45�㣬��thi A��ֵ��
��2����thi A= ![]() �����A=�㣻
�����A=�㣻
��3������A����ǣ�̽��thi A��sinA��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���A=90�㣬��D��E�ֱ���AC��BC�ϣ���CDBC=ACCE����EΪԲ�ģ�DE��Ϊ�뾶��Բ����E������B����AB��BC�ֱ��ڵ�F��G�� 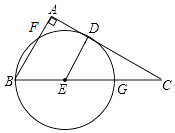
��1����֤��AC�ǡ�E�����ߣ�
��2����AF=4��CG=5�����E�İ뾶��
��3����Rt��ABC������ԲԲ��ΪI����IE= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB=90����AC=BC��AD��CE��BE��CE������ֱ�ΪD��E��
��1��֤������BCE�ա�CAD��
��2����AD=25cm��BE=8cm����DE�ij���
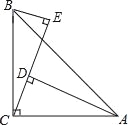
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��24cm�Ŀ������ڵ���ֱ��Ϊ15cm����Ϊ8cm��Բ����ˮ���У������¶�ڱ�������ij���Ϊhcm����h��ȡֵ��Χ���� ��
A. h��17 B. h��8 C. 15��h��16 D. 7��h��16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
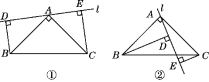
����Ŀ����ͼ�٣���Rt��ABC�У�AB��AC����BAC��90��������A��ֱ��l�Ƶ�A��ת��BD��l��D��CE��l��E.
(1)��˵����DE��BD��CE.
(2)��ֱ��l�Ƶ�A��ת����ͼ����ʾ��λ��ʱ��(1)�н����Ƿ����������������˵����������������̽��DE��BD��CE����������������ϵ����д��̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
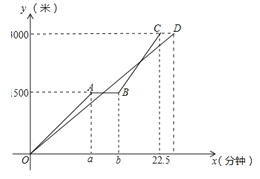
����Ŀ����2017������ʡ��������У���25�⣬10�֣�����̼��������ɫ������������õ����Ⱥ�ڵĽ��ܣ�Խ��Խ������ٴ�ѡ�����г���Ϊ���й��ߣ�С���Ͱְ�ͬʱ�Ӽ������г�ȥͼ��ݣ��ְ�����150��/�ֵ��ٶ�����һ��ʱ�䣬��Ϣ��5���ӣ�����m��/�ֵ��ٶȵ���ͼ��ݣ�С��ʼ����ͬһ�ٶ����У�������ʻ��·��y���ף���ʱ��x�����ӣ��Ĺ�ϵ��ͼ������ͼ����������⣺
��1��a= ��b= ��m= ��
��2����С�����ٶ���120��/�֣���С����;����ְֵڶ�������ʱ����ͼ��ݵľ��룻
��3���ڣ�2���������£��ְ��Եڶ��γ���������ͼ���ǰ����ʱ��С�����100�ף�
��4����С������ʻ�ٶ���v��/�֣�����;����ְ�ǡ���������Σ��������ҡ�ͼ������أ�����ֱ��д��v��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com