
(1)将抛物线y1=2x2向右平移2个单位,得到抛 物线y2的图象,则y2=2(x﹣2)2或2x2﹣8x+8;
物线y2的图象,则y2=2(x﹣2)2或2x2﹣8x+8;
(2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则

t=1,3或 . 解:(1)抛物线y1=2x2向右平移2个单位,得:y=2(x﹣2)2=2x2﹣8x+8;
. 解:(1)抛物线y1=2x2向右平移2个单位,得:y=2(x﹣2)2=2x2﹣8x+8;
故抛物线y2的解析式为y2=2x2﹣8x+8.

(2)由(1)知:抛物线y2的对称轴为x=2,故P点横坐标为2;
当x=t时,直线y=x=t,故A(t,t);
则y2=2x2﹣8x+8=2t2﹣8t+8,故B(t,2t2﹣8t+8);
若△ABP是以点A或点B为直角顶点的等腰直角三角形,则有AB=AP或AB=BP,
此时AB=|2t2﹣8t+8﹣t|,AP=|t﹣2|,
可得:|t﹣2 |=|2t2﹣8t+8﹣t|;
|=|2t2﹣8t+8﹣t|;
当2t2﹣8t+8﹣t=t﹣2时,如图1,t2﹣5t+5=0,解得t1= ;
;
当2t2﹣8t+8﹣t=2﹣t时,如图2,t2﹣4t+3=0,解得t2=1,t3=3;
故符合条件的t值为:1或3或 .
.

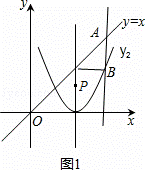


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
某商品的进价为每件30元,现在的售价为每件40元,每星期可卖出150件.市场调查反映:如果每件的售价每涨1元(售价每件不能高于45元),那么每星期少卖10件.设每件涨价x元(x为非负整数),每星期的销量为y件.
(1)求y与x的函数关系式及自变量x的取值范围;
(2)如何定价才能使每星期的利润最大且每星期的销量较大?每星期的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
在实数:3.1415926, ,1.010010001…(每两个1之间依次多一个0),3.
,1.010010001…(每两个1之间依次多一个0),3.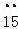 ,
, 中,有理数的个数为( )
中,有理数的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是( )

A.  B. 6 C.
B. 6 C.  D. 3
D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com