
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据直角三角形的判定方法,对选项进行一一分析,选择正确答案.
解答 解:①三角形的一个外角与相邻内角相等可以推出这两个角都是直角,所以这个是直角三角形;
②∠A=$\frac{1}{2}$∠B=$\frac{1}{3}$∠C,又∠A+∠B+∠C=180°可以解出∠C=90°,所以它是直角三角形;
③AC:BC:AB=1:$\sqrt{3}$:2,可推出AC2+BC2=AB2,所以它是直角三角形;
④AC=n2-1,BC=2n,AB=n2+1,可推出AC2+BC2=AB2,所以它是直角三角形.
故选A.
点评 本题考查了直角三角形的判定,包括直角三角形的定义和勾股定理的逆定理,解题关键是熟练掌握勾股定理的逆定理以及三角形内角和等知识.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
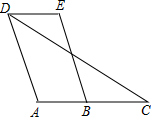 已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.
如图,在Rt△OAB中,∠ABO=90°,点O与原点重合,OB在数轴正半轴上,∠AOB=30°,AB=2,动点P从原点出发,在数轴正半轴上移动,当△OAP为等腰三角形时,P点表示的数是$\frac{4\sqrt{3}}{3}$或4或4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
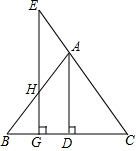 如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.
如图,AD是∠BAC的平分线,且垂直于BC,垂足为D,点E在CA上,EG⊥BC,垂足为点G,交AB于点H.写出图中与∠CEG相等的所有角,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com