
【题目】如图,在![]() 中,
中,![]() ,若有一动点
,若有一动点![]() 从
从![]() 出发,沿
出发,沿![]() 匀速运动,则
匀速运动,则![]() 的长度
的长度![]() 与时间
与时间![]() 之间的关系用图像表示大致是( )
之间的关系用图像表示大致是( )

A.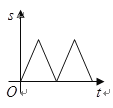 B.
B.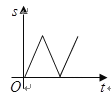
C. D.
D.
科目:初中数学 来源: 题型:
【题目】完成下列证明过程,并在括号内填上依据.
如图,点E在AB上,点F在CD上,∠1=∠2,∠B=∠C,求证AB∥CD.
证明:∵∠1=∠2(已知),∠1=∠4( ),
∴∠2= (等量代换),
∴ ∥BF( ),
∴∠3=∠ ( ).
又∵∠B=∠C(已知),
∴∠3=∠B( ),
∴AB∥CD( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
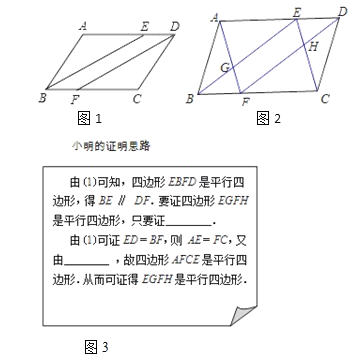
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题一:如图①,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地.若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h),两车之间距离为y(km).
(1)当甲追上乙时,x= .
(2)请用x的代数式表示y.
问题二:如图②,若将上述线段AC弯曲后视作钟表外围的一部分,线段AB正好对应钟表上的弧AB(1小时的间隔),易知∠AOB=30°.
(3)分针OD指向圆周上的点的速度为每分钟转动 km,时针OE指向圆周上的点的速度为每分钟转动 °;
(4)若从2:00起计时,求几分钟后分针与时针第一次重合?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若x,y都是实数,且y=![]() +
+![]() +8,求5x+13y+6的值;
+8,求5x+13y+6的值;
(2)已知△ABC的三边长分别为a,b,c,且满足![]() +b2-6b+9=0,求c的取值范围。
+b2-6b+9=0,求c的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果方程x2+px+q=0的两个根是x1,x2,那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)若p=﹣4,q=3,求方程x2+px+q=0的两根.
(2)已知实数a、b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求![]() +
+![]() 的值;
的值;
(3)已知关于x的方程x2+mx+n=0,(n≠0),求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.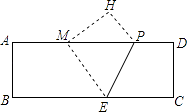
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com