
| |||||||||||
(1) |
证明:连接AC,AD在△ABC与△AED中, 所以△ABC≌△AED(SSS). 所以AC=AD. 在△ACF与△ADF中, 所以△ACF≌△ADF(SSS). 所以∠1=∠2. 又因为∠1+∠2=180°, 所以∠1=∠2=90°. 所以AF⊥CD. 分析:需证AF⊥CD,可考虑证明∠1=90°,由于∠1+∠2=180°,则只需证明∠1=∠2即可,于是要设法找到分别含∠1,∠2的两个全等三角形,只要连接AC,AD,可得到符合要求的△ACF与△ADF.要证明它们全等,只要证明AC=AD就行,可由△ABC≌△AED得到. |
(2) |
证明:连接BE后可得结论有①AF⊥BE;②AF平分∠BAE;③BE∥CD;④∠EBC=∠BED等. 分析:连接BE后,由AF⊥CD联想到AF⊥BE,AF是否平分∠BAE等,并思考所猜想的结论是否成立,从而得到正确结论. |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:新课标 读想练同步测试 七年级数学(下) 北师大版 题型:022
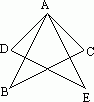
如图所示,AB=AE,AC=AD,只要∠________=∠________或∠________=∠________,就可得△________≌△________.
查看答案和解析>>
科目:初中数学 来源:新教材完全解读 九年级数学 (下册) (配华东师大版新课标) 华东师大版新课标 题型:047
已知如图所示,AB=AE,∠BAE=∠CAD,AC=AD.求证BC=ED.

查看答案和解析>>
科目:初中数学 来源:2011年沈阳招生中考数学试题 题型:选择题
如图所示,AB=AC,要说明△ADC≌△AEB,需添加的条件不能是 ( )

A.∠B=∠C B.AD=AE
C.DC=BE D.∠ADC=∠AEB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com