
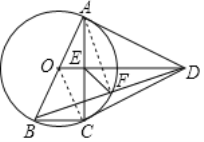
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接 AC、OD交于点E.
(1)若tan∠ABC=2,证明:DA与⊙O相切:
(2)在(1)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.

【答案】(1)证明见解析;(2)EF=![]()
【解析】
(1)连接OC,证△OAD≌△OCD得∠ADO=∠CDO,由AD=CD知DE⊥AC,再由AB为直径知BC⊥AC,从而证明OD∥BC;再根据tan∠ABC=2可设BC=a、则AC=2a、AD=AB=![]() ,证OE为中位线知OE=
,证OE为中位线知OE=![]() a、AE=CE=
a、AE=CE=![]() AC=a,进一步求得DE=
AC=a,进一步求得DE=![]() ,再在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
,再在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
(2)先证△AFD∽△BAD得DFBD=AD2 ①,再证△AED∽△OAD得ODDE=AD2 ②,由①②得DFBD=ODDE,即![]() ,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得
,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得![]() ,结合(1)可得相关线段的长,代入计算可得.
,结合(1)可得相关线段的长,代入计算可得.
解:(1)连接OC,
在△OAD和△OCD中,
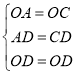 ,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
又AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ACB=90°,即BC⊥AC,
∴OD∥BC,
∵tan∠ABC=![]() ,
,
∴设BC=a、则AC=2a,
∴AD=AB=![]() ,
,
∵OE∥BC,且AO=BO,
∴OE=![]() BC=
BC=![]() a,AE=CE=
a,AE=CE=![]() AC=a,
AC=a,
在△AED中,DE=![]() ,
,
在△AOD中,AO2+AD2=(![]() )2+(
)2+(![]() )2=
)2=![]() ,
,
OD2=(OE+DE)2=(![]() a+2a)2=
a+2a)2=![]() ,
,
∴AO2+AD2=OD2,
∴∠OAD=90°,
则DA与⊙O相切;
(2)连接AF,
∵AB是⊙O的直径,
∴∠AFD=∠BAD=90°,
∵∠ADF=∠BDA,
∴△AFD∽△BAD,
∴![]() ,即DFBD=AD2 ①,
,即DFBD=AD2 ①,
又∵∠AED=∠OAD=90°,∠ADE=∠ODA,
∴△AED∽△OAD,
∴![]() ,即ODDE=AD2 ②,
,即ODDE=AD2 ②,
由①②可得DFBD=ODDE,即![]() ,
,
又∵∠EDF=∠BDO,
∴△EDF∽△BDO,
∵BC=1,
∴AB=AD=![]() ,OD=
,OD=![]() ,ED=2,BD=
,ED=2,BD=![]() ,OB=
,OB=![]() ,
,
∴![]() ,即
,即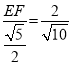 ,
,
解得:EF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,并且∠ABM=2∠BAM.
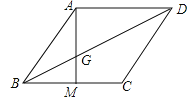
(1)求证:AG=BG;
(2)若点M为BC的中点,同时S△BMG=1,求三角形ADG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图.
(1)参加音乐类活动的学生人数为 人,参加球类活动的人数的百分比为 ;
(2)请把图2(条形统计图)补充完整;
(3)该校学生共600人,则参加棋类活动的人数约为 ;
(4)该班参加舞蹈类活动的4位同学中,有1位男生(用E表示)和3位女生(分别用F,G,H表示),先准备从中选取两名同学组成舞伴,请用列表或画树状图的方法求恰好选中一男一女的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
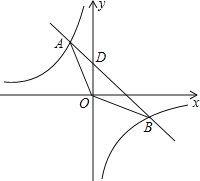
【题目】如图,反比例函数y=﹣![]() 与一次函数y=﹣x+2的图象交于A、B两点.
与一次函数y=﹣x+2的图象交于A、B两点.
(1)试求A、B两点的坐标;
(2)直线AB交y轴于点C,求tan∠AOC的值;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
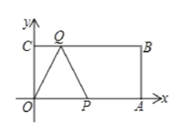
【题目】如图,矩形OABC的边OA在x轴上,OA=10cm,OC在y轴上,且OC=4cm,P为OA 的中点,动点Q从C点出发,沿着CB以每秒1cm的速度运动(Q到B点时停止运动),当△OPQ是以OP为腰的等腰三角形时,点Q的运动时间=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论错误的是( )
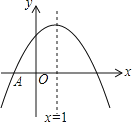
A.3a+b<0B.﹣2≤a≤﹣lC.abc>0D.9a+3b+2c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示的双曲线是函数![]() (m为常数,x>0)图象的一支.
(m为常数,x>0)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与一次函数y=x+1的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,扇形AOB中,∠AOB=120°,OA=2,若以A为圆心,OA长为半径画弧交弧AB于点C,过点C作CD⊥OA,垂足为D,则图中阴影部分的面积为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,点
,点![]() ,直线
,直线![]() ,直线
,直线![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的顶点
的顶点![]() ,且
,且![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,若把抛物线上下平移,使抛物线的顶点在直线
,若把抛物线上下平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ),再把抛物线左右平移,使抛物线的顶点在直线
),再把抛物线左右平移,使抛物线的顶点在直线![]() 上(此时抛物线的顶点记为
上(此时抛物线的顶点记为![]() ).
).
(1)求抛物线![]() 的解析式.
的解析式.
(2)判断以点![]() 为圆心,半径长为4的圆与直线
为圆心,半径长为4的圆与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设点![]() 、
、![]() 在直线
在直线![]() 上(点
上(点![]() 在点
在点![]() 的下方),当
的下方),当![]() 与
与![]() 相似时,求
相似时,求![]() 、
、![]() 的坐标(直接写出结果).
的坐标(直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com