Question

5．某公司员工分别住在A、B、C、D四个住宅区，A区有20人，B区有15人，C区有5人，D区有30人，四个区在同一条直线上，位置如图所示．该公司的接送车打算在此间设立一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设置在（　　）

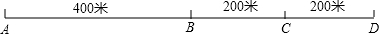
• A． D区
• B． A区
• C． AB两区之间
• D． BC两区之间

Answer 1

分析 根据题意分别计算停靠点分别在各点是员工步行的路程和，选择最小的即可解答．

解答 解：∵当停靠点在D区时，所有员工步行到停靠点路程和是：20×800+15×400+5×200=23000m；
当停靠点在A区时，所有员工步行到停靠点路程和是：15×400+5×600+30×800=33000m；
当停靠点在AB两区之间时，设距离B区x米，所有员工步行到停靠点路程和是：20×（400-x）+15x+5×（200+x）+30×（400+x）=（30x+21000）m；
当停靠点在BC两区之间时，设距离B区x米，所有员工步行到停靠点路程和是：20×（400+x）+15x+5×（200-x）+30×（400-x）=21000m．
∴当停靠点在BC两区之间时，所有员工步行到停靠点路程和最小，那么停靠点的位置应该在BC两区之间．
故选D．

点评 此题考查了比较线段的长短，正确理解题意是解题的关键．要能把线段的概念在现实中进行应用．