
【题目】在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.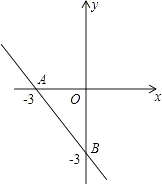
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.
【答案】
(1)
解:A(﹣3,0),B(0,﹣3)代入y=kx+b得
![]() ,解得
,解得 ![]() ,
,
∴一次函数y=kx+b的解析式为:y=﹣x﹣3
(2)
解:二次函数y=x2+mx+n图象的顶点为(﹣ ![]() ,
, ![]() )
)
∵顶点在直线AB上,
∴ ![]() =
= ![]() ﹣3,
﹣3,
又∵二次函数y=x2+mx+n的图象经过点A(﹣3,0),
∴9﹣3m+n=0,
∴组成方程组为 
解得 ![]() 或
或 ![]()
(3)
解:∵二次函数y=x2+mx+n的图象经过点A.
∴9﹣3m+n=0,
∵当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,
①如图1,当对称轴﹣3<﹣ ![]() <0时
<0时
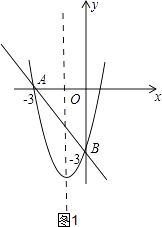
最小值为 ![]() =﹣4,与9﹣3m+n=0,组成方程组为
=﹣4,与9﹣3m+n=0,组成方程组为
 解得
解得 ![]() 或
或 ![]() (由﹣3<﹣
(由﹣3<﹣ ![]() <0知不符合题意舍去)
<0知不符合题意舍去)
所以 ![]() .
.
②如图2,当对称轴﹣ ![]() >0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
>0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,

把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() >0,
>0,
∴m<0,
∴此种情况不成立,
③当对称轴﹣ ![]() =0时,y=x2+mx+n的最小值为﹣4,
=0时,y=x2+mx+n的最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入9﹣3m+n=0,得m= ![]() .
.
∵﹣ ![]() =0,
=0,
∴m=0,
∴此种情况不成立,
④当对称轴﹣ ![]() ≤﹣3时,最小值为0,不成立
≤﹣3时,最小值为0,不成立
综上所述m=2,n=﹣3.
【解析】(1)利用待定系数法求出解析式,(2)先表示出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值,(3)本题要分四种情况①当对称轴﹣3<﹣ ![]() <0时,②当对称轴﹣
<0时,②当对称轴﹣ ![]() >0时,③当对称轴﹣
>0时,③当对称轴﹣ ![]() =0时,④当对称轴﹣
=0时,④当对称轴﹣ ![]() ≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
≤﹣3时,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n但一定要验证是否符合题意.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( ) 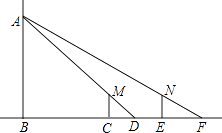
A.4.5米
B.6米
C.7.2米
D.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC. 
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的已知、求证,并完成证明过程.
(1)命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).
已知:如图, .
求证: .
(2)证明命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的已知、求证,并完成证明过程.
(1)命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).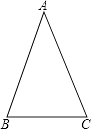
已知:如图, .
求证: .
(2)证明命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,互联网消费逐渐深入人们的生活,如图所示的是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,有下列说法:其中正确说法的个数有( ) ①“快车”行驶里程不超过5公里计费8元;
②“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
③A点的坐标为(6.5,10.4);
④从合肥西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q. 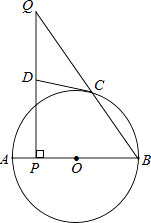
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ![]() ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=﹣ ![]() 的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 .
的图象上的一个动点,连接OA,若将线段O A绕点O顺时针旋转90°得到线段OB,则点B所在图象的函数表达式为 . 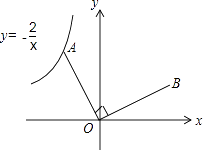
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com