
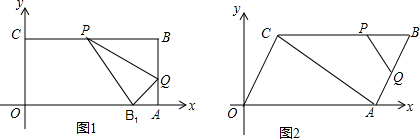
分析 (1)①根据OA=4,OC=2,可得点B的坐标;
②首先设AQ=x,由点B关于PQ的对称点为B1,可得B1Q=BQ=2-x,然后由在Rt△AB1Q中,由AQ2+AB12=B1Q2,得方程:x2+1=(2-x)2,解此方程解可求得答案;
(2)根据平行四边形的性质,且分点在线段EF的延长线和线段上两种情况进行分析求解可求得答案.
解答 解:(1)∵OA=4,OC=2,
∴点B的坐标为(4,2);
②设AQ=x,点B关于PQ的对称点为B1,则B1Q=BQ=2-x,
∵点B1落在OA上,点B1(3,0),
∴OB1=3,
∴AB1=4-3=1,
在Rt△AB1Q中,由AQ2+AB12=B1Q2,
得:x2+1=(2-x)2,
解得:x=$\frac{3}{4}$;
∴点Q的坐标为:(4,$\frac{3}{4}$);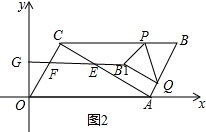
(2)∵四边形OABC为平行四边形,OA=4,OC=2,且OC⊥AC,
∴∠OAC=30°,
∴点C(1,$\sqrt{3}$),
∵B1F=3B1E,
∴点B1不与点E,F重合,也不在线段EF的延长线上,
①当点B1在线段FE的延长线上时,如图2,延长B1F与y轴交于点G,点B1的横坐标为m,B1F∥x轴,
∵B1F=3B1E,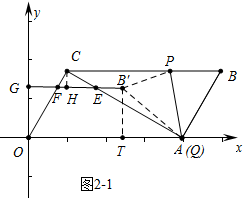
∴B1G=m,
设OG=a,
则GF=$\frac{\sqrt{3}}{3}$a,OF=$\frac{2\sqrt{3}}{3}$a,
∴CF=2-$\frac{2\sqrt{3}}{3}$a,
∴EF=4-$\frac{4\sqrt{3}}{3}$a,B1E=2-$\frac{2\sqrt{3}}{3}$a,
∴B1G=B1E+EF+FG=(2-$\frac{2\sqrt{3}}{3}$a)+(4-$\frac{4\sqrt{3}}{3}$a)+$\frac{\sqrt{3}}{3}$a=m,
∴a=-$\frac{\sqrt{3}}{5}$m+$\frac{6}{5}$$\sqrt{3}$,即B1的纵坐标为-$\frac{\sqrt{3}}{5}$m+$\frac{6}{5}$$\sqrt{3}$,
如图2-1中,当点Q与A重合时,可得点B′横坐标的最小值,
作CH⊥EF于H,B′T⊥OA于T,设FH=n,则CF=2n,EF=4n,EB′=2n,OF=2-2n,FG=1-n,GB=1+5n,
在Rt△AB′T中,易知TB′=OG=$\sqrt{3}$(1-n),AB′=2,AT=4-(1+5n)=3-5n,
∴[$\sqrt{3}$(1-n)]2+(3-5n)2=22,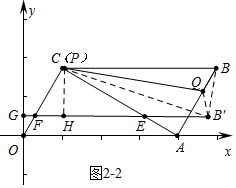
解得n=$\frac{2}{7}$或-1(舍弃),
∴GB′=1+$\frac{10}{7}$=$\frac{17}{7}$,
如图2-2中,当点P与C重合时,可得点B′横坐标的最大值,
作CH⊥EF于H,设FH=n,则CF=2n,EF=4n,EB′=2n,OF=2-2n,FG=1-n,GB=1+5n,
在Rt△CB′H中,易知CH=$\sqrt{3}$n,HB′=5n,CB′=CB=4,
∴($\sqrt{3}$n)2+(5n)2=42,
解得n=$\frac{2\sqrt{7}}{7}$
∴GB′=1+5n=1+$\frac{10\sqrt{7}}{7}$
∴m的取值范围是$\frac{17}{7}$≤m≤1+$\frac{10}{7}$$\sqrt{7}$; ②当点B1在线段EF(除点E,F)上时,如图3,延长B1F与y轴交于点G,点B1的横坐标为m,B1F∥x轴,
②当点B1在线段EF(除点E,F)上时,如图3,延长B1F与y轴交于点G,点B1的横坐标为m,B1F∥x轴,
B1F=3B1E,
∴B1G=m,
设OG=a,
则GF=$\frac{\sqrt{3}}{3}$a,OF=$\frac{2\sqrt{3}}{3}$a,
∴CF=2-$\frac{2\sqrt{3}}{3}$a,
∴FE=4-$\frac{4\sqrt{3}}{3}$,B1F=$\frac{3}{4}$EF=3-$\sqrt{3}$a,
∴B1G=B1F+FG=(3-$\sqrt{3}$a)+$\frac{\sqrt{3}}{3}$a=m,
∴a=-$\frac{\sqrt{3}}{2}$m+$\frac{3}{2}$$\sqrt{3}$,即点B1的纵坐标为-$\frac{\sqrt{3}}{2}$m+$\frac{3}{2}$$\sqrt{3}$,
同法可求m的取值范围是:$\frac{15}{7}$≤m≤3.
∴m的最大值为:1+$\frac{10}{7}$$\sqrt{7}$,最小值为:$\frac{15}{7}$.
点评 此题属于四边形的综合题.考查了矩形的性质、平行四边形的性质以及勾股定理等知识.解题的关键是利用平行四边形的性质,分点在线段EF的延长线和线段上两种情况进行分析求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
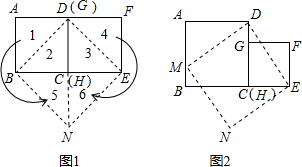
 如图在△ABC中,AB=AC,∠A=120°,BC=9cm,AB的垂直平分线交BC于点M,交AB于点N,AC的垂直平分线交BC于点E,交AC于点F,则ME的长是( )
如图在△ABC中,AB=AC,∠A=120°,BC=9cm,AB的垂直平分线交BC于点M,交AB于点N,AC的垂直平分线交BC于点E,交AC于点F,则ME的长是( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≠1 | B. | a>-1且a≠1 | C. | a≥-1且a≠1 | D. | a为任意实数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
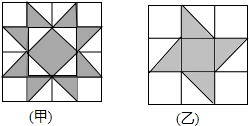 如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )
如图是甲、乙两种地板,它们都是由等腰直角三角形和正方形的地砖拼成,且直角边与正方形边的长相等,一个小球分别在这两种地板上自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则P1与P2的大小关系是( )| A. | P1<P2 | B. | P1=P2 | C. | P1>P2 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com