
分析 由$\frac{a-2b}{2a+b}$=$\frac{1}{5}$得:a=$\frac{11}{3}$b,把它们代入原式合并后约分即可,由a:b:c=3:2:5,设a=3k,b=2k,c=5k,然后把它们代入原式合并后约分即可.
解答 解:由$\frac{a-2b}{2a+b}$=$\frac{1}{5}$得:a=$\frac{11}{3}$b,$\frac{a}{b}$=$\frac{\frac{11}{3}b}{b}$=$\frac{11}{3}$,
由a:b:c=3:2:5,设a=3k,b=2k,c=5k,则$\frac{a+2b-c}{a-b+c}$=$\frac{2k}{6k}$=$\frac{1}{3}$,
故答案为:$\frac{11}{3}$,$\frac{1}{3}$.
点评 本题考查了比例的性质:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
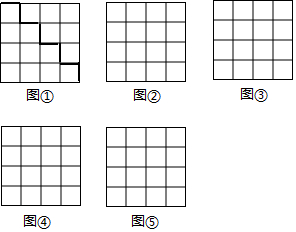 如图(1),把大小为4×4的正方形方格图形分割成两个全等图形,请在图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.
如图(1),把大小为4×4的正方形方格图形分割成两个全等图形,请在图中,沿着虚线画出四种不同的分法,把4×4的正方形方格图形分割成两个全等图形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
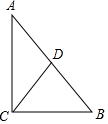 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
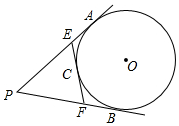 如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4.
如图,PA,PB是圆O的切线,切点为分别A,B,圆O的切线EF分别交PA,PB于点E,F,切点C在弧$\widehat{AB}$上,若PA长为2,则△PEF的周长是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com