
 ��
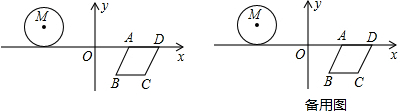
�� ���� ��1������B��BE��AD������ΪE���ɵ�A�͵�B�������֪��BE=$\sqrt{3}$��AE=1�����ݹ��ɶ��������AB�ij����Ӷ���������ε��ܳ���
��2���ǡ�M��x�������ΪF��AD���е�ΪE�������EF�ij���Ȼ�����·��=ʱ����ٶ��г����̼��ɣ�ƽ�Ƶ�ͼ����ͼ3��ʾ������B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮������������Ǻ���ֵ����á�EAB=60�㣬�������ε����ʿɵõ���FAC=60�㣬Ȼ��֤����AFM�ǵ���ֱ�������Σ��Ӷ��ɵõ���MAF�Ķ������ʴ˿���á�MAC�Ķ�����
��3���������ε����ʺ����ߵ����ʣ���������������AE���ɵó�ʱ��t��
��� �⣺��1������B��BE��AD������ΪE��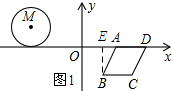
��B��1��-$\sqrt{3}$����A��2��0����
��BE=$\sqrt{3}$��AE=1��
��AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=2��
���ı���ABCDΪ���Σ�
��AB=BC=CD=AD��
�����ε��ܳ�=2��4=8��
��2����ͼ2��ʾ����M��x�������ΪF��AD���е�ΪE��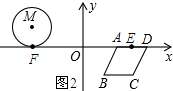
��M��-3��1����
��F��-3��0����
��AD=2����EΪAD���е㣬
��E��3��0����
��EF=6��
��2t+3t=6��
��ã�t=$\frac{6}{5}$��
ƽ�Ƶ�ͼ����ͼ3��ʾ��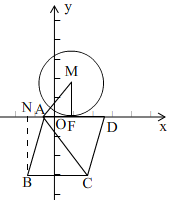
����B��BE��AD������ΪE������MF��FΪ��M��AD���е㣮
���ɣ�1����֪��AN=1��BN=$\sqrt{3}$��
��tan��NAB=$\sqrt{3}$��
���NAB=60�㣮
���FAB=120�㣮
���ı���ABCD�����Σ�
���FAC=$\frac{1}{2}$��FAB=$\frac{1}{2}$��120��=60�㣮
��ADΪ��M�����ߣ�
��MF��AD��
��FΪAD���е㣬
��AF=MF=1��
���AFMΪ����ֱ�������Σ�
���MAF=45�㣮
���MAC=��MAF+��FAC=45��+60��=105�㣮
��3����ͼ4��ʾ��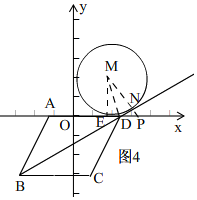
����DM������M��MN��BD������ΪN�����ӳ���x����P����ME��AD������ΪE��
���ı���ABCDΪ���Σ���DAB=120�㣬
���PDN=��ADB=30�㣮
��BD��AD�ǡ�M�����ߣ�
���PME=30��
��ME=1��
��Rt��PME��PM=$\frac{2\sqrt{3}}{3}$��PE=$\frac{\sqrt{3}}{3}$��
��Rt��PDN��PN=PM-1=$\frac{2\sqrt{3}}{3}$-1��
��PD=2PN=$\frac{4\sqrt{3}}{3}$-2��
��DE=PE-PD=2-$\sqrt{3}$��
��EA=5+2-��2-$\sqrt{3}$��=5+$\sqrt{3}$��
��3t+2t=5+$\sqrt{3}$��
��t=1+$\frac{\sqrt{3}}{5}$��
��ͼ5��ʾ������AM��������MN��AC������ΪN����ME��AD������ΪE��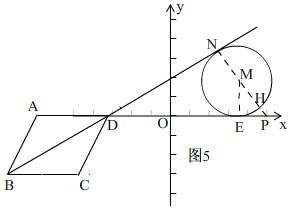
���ı���ABCDΪ���Σ���DAB=120�㣬
���PDN=��ADB=30�㣮
��BD��AD�ǡ�M�����ߣ�
���PME=30�㣮
��ME=1��
��Rt��PME��PM=$\frac{2\sqrt{3}}{3}$��PE=$\frac{\sqrt{3}}{3}$��
��Rt��PDN��PN=PM+1=$\frac{2\sqrt{3}}{3}$+1��
��PD=2PN=$\frac{4\sqrt{3}}{3}$+2��
��DE=PD-PE=2+$\sqrt{3}$��
��EA=5+2+��2-$\sqrt{3}$��=9-$\sqrt{3}$��
��3t+2t=9-$\sqrt{3}$��
��t=$\frac{9}{5}$+$\frac{\sqrt{3}}{5}$��
����������t=1+$\frac{\sqrt{3}}{5}$��t=$\frac{9}{5}$+$\frac{\sqrt{3}}{5}$ʱ����M��AC���У�
���� ������Բ���ۺ��⣬��ҪӦ�������ߵ����ʡ����߳����������ε����ʡ�����������Ǻ���ֵ�����ɶ�����Ӧ�ø��������г�����t�ķ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2000 | B�� | -1 | C�� | 1 | D�� | 2016 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
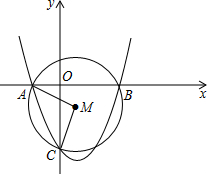 ��ͼ�����κ���y=x2-2x-3��ͼ����a��0����B��b��0����C��0��c�����㣬��a��b��
��ͼ�����κ���y=x2-2x-3��ͼ����a��0����B��b��0����C��0��c�����㣬��a��b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com