
【题目】如图,直线AB、CD相交于点O,EO⊥AB,垂足为O,∠EOC:∠AOD=7:11,求∠DOE的度数. 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如果规定收入为正,支出为负,收入200元记作+200元,那么支出37元记作( )
A. 200元 B. -37元 C. 163元 D. 37元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2 , 长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由. 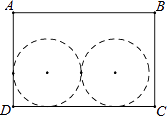
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 且l4和l1、l2分别交于A、B两点,点P为线段AB上的一个定点如图1) 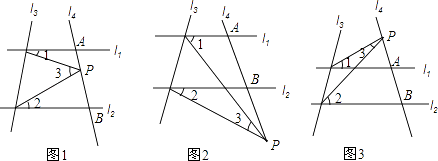
(1)写出∠1、∠2、∠3、之间的关系并说出理由.
(2)如果点P为线段AB上的动点时,问∠1、∠2、∠3之间的关系是否发生变化?(必说理由)
(3)如果点P在A、B两点外侧运动时,(点P和点A、点B不重合)
①如图2,当点P在射线AB上运动时,∠1、∠2、∠3之间关系并说出理由.
②如图3,当点P在射线BA上运动时,∠1、∠2、∠3之间关系(不说理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com