
【题目】如图,反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标是
的横坐标是![]() ,点
,点![]() 是第一象限内反比例函数图像上的动点,且在直线
是第一象限内反比例函数图像上的动点,且在直线![]() 的上方.
的上方.
(1)若点![]() 的坐标是
的坐标是![]() ,则
,则![]() ,
,![]() ;
;
(2)设直线![]() 与
与![]() 轴分别交于
轴分别交于![]() 点,求证:
点,求证:![]() 是等腰三角形;
是等腰三角形;
(3)设点![]() 是反比例函数图像位于
是反比例函数图像位于![]() 之间的动点(与点
之间的动点(与点![]() 不重合),连接
不重合),连接![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.

【答案】(1)![]() ,
, ![]() .(2)详见解析;(3)
.(2)详见解析;(3)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)由P点坐标可直接求得k的值,过P、B两点,构造矩形,利用面积的和差可求得△PBO的面积,利用对称,则可求得△PAB的面积;
(2)可设出P点坐标,表示出直线PA、PB的解析式,则可表示出M、N的坐标,作PG⊥x轴于点G,可求得MG=NG,即G为MN的中点,则可证得结论;
(3)连接QA交x轴于点M′,连接QB并延长交x轴于点N′,利用(2)的结论可求得∠MM′A=∠QN′O,结合(2)可得到∠PMN=∠PNM,利用外角的性质及对顶角进一步可求得∠PAQ=∠PBQ.
(1)∵点P(1,4)在反比例函数图象上,
∴k=4×1=4,
∵B点横坐标为4,
∴B(4,1),
连接OP,过P作x轴的平行线,交y轴于点P′,过B作y轴的平行线,交x轴于点B′,两线交于点D,如图1,

则D(4,4),
∴PP′=1,P′O=4,OB′=4,BB′=1,
∴BD=4-1=3,PD=4-1=3,
∴S△POB=S矩形OB′DP′-S△PP′O-S△BB′O-S△BDP=16-2-2-4.5=7.5,
∵A、B关于原点对称,
∴OA=OB,
∴S△PAO=S△PBO,
∴S△PAB=2S△PBO=15;
(2)∵点P是第一象限内反比例函数图象上的动点,且在直线AB的上方,
∴可设点P坐标为(m,![]() ),且可知A(-4,-1),
),且可知A(-4,-1),
设直线PA解析式为y=k′x+b,
把A、P坐标代入可得 ,解得
,解得 ,
,
∴直线PA解析式为![]() ,令y=0可求得x=m-4,
,令y=0可求得x=m-4,
∴M(m-4,0),
同理可求得直线PB解析式为![]() ,令y=0可求得x=m+4,
,令y=0可求得x=m+4,
∴N(m+4,0),
作PG⊥x轴于点G,如图2,则G(m,0),

∴MG=m-(m-4)=4,NG=m+4-m=4,
∴MG=NG,即G为MN中点,
∴PG垂直平分MN,
∴PM=PN,即△PMN是等腰三角形;
(3)∠PAQ=∠PBQ,理由如下:
连接QA交x轴于M′,连接QB并延长交x轴于点N′,如图3,

由(2)可得PM′=PN′,即∠QM′O=∠QN′O,
∴∠MM′A=∠QN′O,
由(2)知∠PMN=∠PNM,
∴∠PMN-∠MM′A=∠PNM-∠QN′O,
∴∠PAQ=∠NBN′,
又∠NBN′=∠PBQ,
∴∠PAQ=∠PBQ.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=![]() ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面,观察下列图形,探究并解答问题:
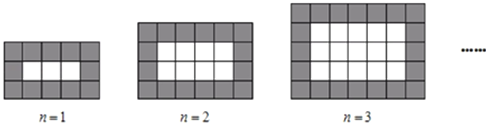
(1)在第4个图中,共有白色瓷砖______块;在第![]() 个图中,共有白色瓷砖_____块;
个图中,共有白色瓷砖_____块;
(2)试用含![]() 的代数式表示在第
的代数式表示在第![]() 个图中共有瓷砖的块数;
个图中共有瓷砖的块数;
(3)如果每块黑瓷砖35元,每块白瓷砖50元,当![]() 时,求铺设长方形地面共需花多少钱购买瓷砖?
时,求铺设长方形地面共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)有理数对(2,-3)★(3,-2)=_______;
(2)若有理数对(-3,2x-1)★(1,x+1)=7,则x=_______;
(3)当满足等式(-3,2x-1)★(k,x+k)=5+2k的x是整数时,求整数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
小红同学在学习过程中遇到这样一道计算题“计算4×2.112-4×2.11×2.22+2.222”,她觉得太麻烦,估计应该有可以简化计算的方法,就去请教崔老师.崔老师说:你完成下面的问题后就可能知道该如何简化计算啦!
获取新知:
请你和小红一起完成崔老师提供的问题:
(1)填写下表:
x=-1,y=1 | x=1,y=0 | x=3,y=2 | x=2,y=-1 | x=2,y=3 | |
A=2x-y | -3 | 2 | 4 | 5 | 1 |
B=4x2-4xy+y2 | 9 | 4 | 16 |
(2)观察表格,你发现A与B有什么关系?
解决问题:
(3)请利用A与B之间的关系计算:4×2.112-4×2.11×2.22+2.222.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=BC=5,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,三角板的两直角边分别交直线AB、BC于E、F两点.
(1)如图①,若O为AC的中点,点E、F分别在边AB、BC上.
①当△OFC是等腰直角三角形时,∠FOC= ;
②求证:OE=OF;
(2)如图②,若AO:AC=1:4时,OE和OF有怎样的数量关系?证明你发现的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com