
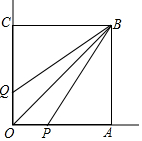
 如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15.
如图,正方形OABC的边长为3,点P与点Q分别在射线OA与射线OC上,且满足BP=BQ,若AP=2,则四边形OPBQ面积的值可能为3或9或15. 分析 如图PA=AP′=2,CQ=CQ′=2,①四边形OPBQ的面积=2×$\frac{1}{2}$×1×3=3.②四边形OP′BQ的面积=$\frac{1}{2}$×1×3+$\frac{1}{2}$×5×3=9,③四边形OPBQ′的面积=9.④四边形OP′BQ′的面积=2×$\frac{1}{2}$×5×3=15.四边形有四种可能,面积的值有三种可能.
解答 解: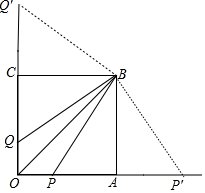
如图PA=AP′=2,CQ=CQ′=2,
①四边形OPBQ的面积=2×$\frac{1}{2}$×1×3=3.
②四边形OP′BQ的面积=$\frac{1}{2}$×1×3+$\frac{1}{2}$×5×3=9,
③四边形OPBQ′的面积=9.
④四边形OP′BQ′的面积=2×$\frac{1}{2}$×5×3=15.
∴四边形OPBQ的面积的值有三种可能.
故答案为3或9或15
点评 本题考查正方形的性质、三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
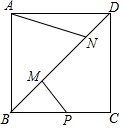 如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )
如图,正方形ABCD的对角线上的两个动点M、N,满足AB=$\sqrt{2}$MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM的最小值时,线段AN的长度为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 6 | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=2,n=-1 | B. | m=-2,n=-1 | C. | m=2,n=1 | D. | m=-2,n=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com