
分析 根据加权平均数的计算方法:先求出所有苹果的总钱数,再除以苹果的总质量,可得混合后的单价;若甲种苹果与乙种苹果数量相等,可把单价定为3元/千克,否则不合理.
解答 解:∵甲种苹果共有a千克,售价为2元/千克,乙种苹果共有b千克,售价为4元/千克,
∴想把这两种苹果混在一起卖,混合后的单价是:$\frac{2a+4b}{a+b}$元;
∵当a=b时,$\frac{2a+4b}{a+b}$=3,
当a≠b时,$\frac{2a+4b}{a+b}$≠3,
∴若他把单价定为3元/千克,我认为不合理.
点评 本题考查的是加权平均数的求法.本题易出现的错误是对加权平均数的理解不正确,而求2,4这两个数的平均数.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:选择题
| A. | k>$\frac{4}{3}$且k≠2 | B. | k≥$\frac{4}{3}$且k≠2 | C. | k>$\frac{3}{4}$且k≠2 | D. | k≥$\frac{3}{4}$且k≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗
一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),在清洗过程中,突然停电了,小伟只好摸黑清洗查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.
如图所示,A(8,0),B点在第一象限,且△AOB是等边三角形,过B点作直线BC∥x轴,交y轴于点C,动点P从C点出发,以每秒1个单位的速度向C点右侧水平方向平移,过P点作DE∥y轴,交直线AB于D,交直线OB于点E,设P点出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
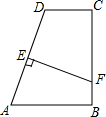 如图,在四边形ABCD中,∠B=∠C=90°,点E是AD的中点,EF⊥AD交CB于点F,DC=6,AB=8,BC=10,则线段BF的长为( )
如图,在四边形ABCD中,∠B=∠C=90°,点E是AD的中点,EF⊥AD交CB于点F,DC=6,AB=8,BC=10,则线段BF的长为( )| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{36}{5}$ | D. | $\frac{18}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com