

分析 猜想:首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
探究:根据菱形的性质得到AD∥BC,AO=CO,BO=$\frac{1}{2}$BD=4,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
应用:延长AC到E使CE=AC=4,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=3,即可得到结论.
解答 解:猜想:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{∠AEO=∠CFO}\\{AO=CO}\end{array}\right.$,
∴△AEO≌△CFO,
∴四边形CDEF的面积=S△ACD=$\frac{1}{2}$?ABCD的面积=5;
故答案为:5;
探究:∵四边形ABCD是菱形,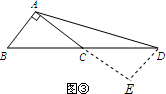
∴AD∥BC,AO=CO,BO=$\frac{1}{2}$BD=4,
∴∠OAE=∠OCF,∠OEA=∠OFC,
在△AOE于△COF中,$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{∠AEO=∠CFO}\\{AO=CO}\end{array}\right.$,
∴△AOE≌△COF,
∵AC⊥BD,
∴${S_{四边形ABFE}}={S_{△ABC}}=\frac{1}{2}AC•BO=\frac{1}{2}×4×4=8$.
应用:延长AC到E使CE=AC=4,
在△ABC与△CDE中,$\left\{\begin{array}{l}{AC=CE}\\{∠ACB=∠DCE}\\{BC=CD}\end{array}\right.$,
∴△ABC≌△CDE,
∴∠E=∠BAC=90°,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=3,
∴S△ABD=S△ADE=$\frac{1}{2}$AE•DE=$\frac{1}{2}$×8×3=12.
故答案为:12.
点评 本题考查了全等三角形的判定和性质,平行四边形的性质,菱形的性质,图形面积的计算,熟练掌握全等三角形的判定和性质是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
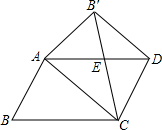 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
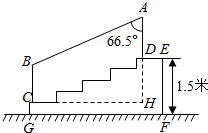 如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com