
【题目】如图,已知直线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,
点,![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动,问
两点除外)上运动,问![]() ,
,![]() ,
,![]() 之间的关系是什么?这种关系是否变化?
之间的关系是什么?这种关系是否变化?
(2)若![]() 点在线段
点在线段![]() 之外时,
之外时,![]() ,
,![]() ,
,![]() 之间的关系怎样?说明理由
之间的关系怎样?说明理由
【答案】(1)∠APB=∠PAC +∠PBD,不会变化;(2)∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB,理由见解析.
【解析】
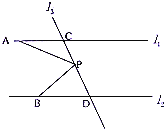
(1)当P点在C、D之间运动时,首先过点P作PE∥l1,由l1∥l2,可得PE∥l2∥l1,根据两直线平行,内错角相等,即可求得:∠APB=∠PAC+∠PBD,即∠APB、∠PAC、∠PBD之间的关系不发生变化;
(2)当点P在C、D两点的外侧运动时,由直线l1∥l2,根据两直线平行,同位角相等以及三角形外角的性质,即可求得∠PAC,∠APB,∠PBD之间的关系.
(1)如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:过点P作PE∥l1,

∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD,
即∠APB、∠PAC、∠PBD之间的关系不发生变化;
(2)如图②,

当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
如图③,

理由如下:∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.


科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件。
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?
(2)若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)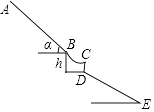
A.101.4
B.101.3
C.100.4
D.100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.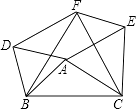
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
![]()
(1)用“<”连接0,a, b, —1
(2)|b-1|+|a-1|=___
(3)化简|a —b|+|a-c|-|b|+|b-c|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
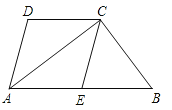
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新兴服装厂生产一种夹克和T恤,夹克每件定价![]() 元,T恤每件定价
元,T恤每件定价![]() 元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的
元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一件夹克送一件T恤;②夹克和T恤都按定价的![]() 付款.现某客户要到该服装厂购买夹克
付款.现某客户要到该服装厂购买夹克![]() 件,T恤
件,T恤![]() 件(
件(![]() ).
).
(1)若该客户按方案①购买,夹克需付款________元,T恤需付款________元(用含![]() 的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含
的式子表示);若该客户按方案②购买,夹克需付款______元,T恤需付款______元(用含![]() 的式子表示);
的式子表示);
(2)若![]() ,通过计算说明按方案①、方案②哪种方案购买较为合算?
,通过计算说明按方案①、方案②哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com