
【题目】如图,⊙O的半径r=25,四边形ABCD内接于圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD. 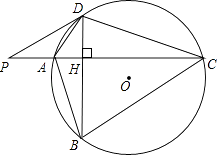
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB= ![]() ,PA=
,PA= ![]() AH,求BD的长;
AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积.
【答案】
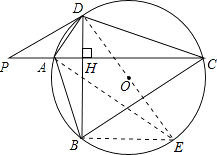
(1)解:PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,
∵DE是直径,
∴∠DAE=90°,
∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,
∴∠PDA+∠ADE=90°,
即PD⊥DO,
∴PD与圆O相切于点D
(2)解:∵tan∠ADB= ![]()
∴可设AH=3k,则DH=4k,
∵PA= ![]() AH,
AH,
∴PA=(4 ![]() ﹣3)k,
﹣3)k,
∴PH=4 ![]() k,
k,
∴在Rt△PDH中,tan∠P= ![]() =
= ![]() ,
,
∴∠P=30°,∠PDH=60°,
∵PD⊥DO,
∴∠BDE=90°﹣∠PDH=30°,
连接BE,则∠DBE=90°,DE=2r=50,
∴BD=DEcos30°= ![]() ;
;
(3)解:由(2)知,BH= ![]() ﹣4k,
﹣4k,
∴HC= ![]() (
( ![]() ﹣4k),
﹣4k),
又∵PD2=PA×PC,
∴(8k)2=(4 ![]() ﹣3)k×[4
﹣3)k×[4 ![]() k+
k+ ![]() (25
(25 ![]() ﹣4k)],
﹣4k)],
解得:k=4 ![]() ﹣3,
﹣3,
∴AC=3k+ ![]() (25
(25 ![]() ﹣4k)=24
﹣4k)=24 ![]() +7,
+7,
∴S四边形ABCD= ![]() BDAC=
BDAC= ![]() ×25
×25 ![]() ×(24
×(24 ![]() +7)=900+
+7)=900+ ![]() .
.
【解析】(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;(2)首先由tan∠ADB= ![]() ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA= ![]() AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DEcos30°=
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DEcos30°= ![]() ;(3)由(2)易得HC=
;(3)由(2)易得HC= ![]() (
( ![]() ﹣4k),又由PD2=PA×PC,可得方程:(8k)2=(4
﹣4k),又由PD2=PA×PC,可得方程:(8k)2=(4 ![]() ﹣3)k×[4
﹣3)k×[4 ![]() k+
k+ ![]() (25
(25 ![]() ﹣4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.
﹣4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.


科目:初中数学 来源: 题型:
【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.符合题意的组建方案有( )种.
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
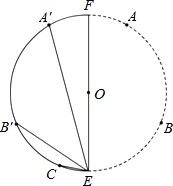
【题目】如图,A,B,C为⊙O上相邻的三个n等分点, ![]() ,点E在
,点E在 ![]() 上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°=
上,EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′.设EB′=b,EC=c,EA′=p.现探究b,c,p三者的数量关系:发现当n=3时,p=b+c.请继续探究b,c,p三者的数量关系:当n=4时,p=;当n=12时,p= . (参考数据:sin15°=cos75°= ![]() ,cos15°=sin75°=
,cos15°=sin75°= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
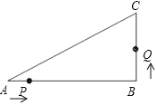
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为_____________.(点C不与点A重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4 个小长方形,然后按图2的形状拼成一个正方形.
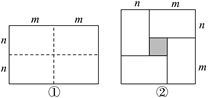
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com