
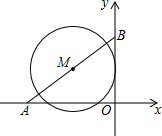
 如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由.
如图直角坐标系中,已知A(-8,0),B(0,6),点M在线段AB上.如果点M是线段AB的中点,且⊙M的半径为4,试判断直线OB与⊙M的位置关系,并说明理由.  全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -4 | +12 | -10 | +16 | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)
如图,在矩形ABCD中,AB=2cm,BC=4cm,点P从点A出发,沿AB以1cm/s的速度向点B匀速运动,同时点Q从点D出发,沿D-C-B以3cm/s的速度向点B匀速运动,连接PQ、BQ,设点P的运动时间为t(s),△BPQ的面积为S(cm2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m÷n•m=m | B. | m÷n•$\frac{1}{m}$=m | C. | $\frac{1}{m}$÷m•m=1 | D. | n÷m•m=n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com