
【题目】问题情景:如图1,AB∥CD,∠PAB=140°,∠PCD=135°,求∠APC的度数.
(1)丽丽同学看过图形后立即口答出:∠APC=85°,请你补全她的推理依据.
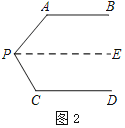
如图2,过点P作PE∥AB,
∵AB∥CD,∴PE∥CD. ( )
∴∠A+∠APE=180°.
∠C+∠CPE=180°. ( )
∵∠PAB=140°,∠PCD=135°,
∴∠APE=40°,∠CPE=45°
∴∠APC=∠APE+∠CPE=85°.( )
问题迁移:
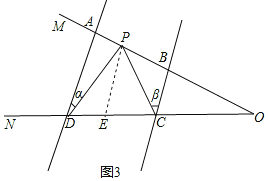
(2)如图3,AD∥BC,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β,求∠CPD与∠α、∠β之间有何数量关系?请说明理由.
(3)在(2)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD与∠α、∠β之间的数量关系.

【答案】(1)平行于同一条直线的两条直线平行;两直线平行,同旁内角互补;等量代换;(2)∠CPD=∠α+∠β,理由见解析;(3)当P在BA延长线时,∠CPD=∠β﹣∠α;当P在AB延长线时,∠CPD=∠α﹣∠β.
【解析】(1) 过点P作PE∥AB,根据“两直线平行,同旁内角互补”可得∠A+∠APE=180°,∠C+∠CPE=180°;进一步可求得结果.(2)过P作PE∥AD交CD于E,则AD∥PE∥BC,根据“两直线平行,内错角相等”可得∠α=∠DPE,∠β=∠CPE,因此,∠CPD=∠DPE+∠CPE=∠α+∠β;(3)类似(2)的方法,分两种情况,即:P在BA延长线时或在AB延长线时.可得出结论..
解:(1)过点P作PE∥AB,
如图2所示:
∵AB∥CD,
∴PE∥CD.(平行于同一条直线的两条直线平行)
∴∠A+∠APE=180°.
∠C+∠CPE=180°.(两直线平行同旁内角互补)
∵∠PAB=140°,∠PCD=135°,
∴∠APE=40°,∠CPE=45°,
∴∠APC=∠APE+∠CPE=85°.(等量代换)
故答案为:平行于同一条直线的两条直线平行;两直线平行,同旁内角互补;等量代换;
(2)∠CPD=∠α+∠β,理由如下:
如图3所示,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
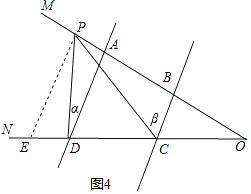
(3)当P在BA延长线时,如图4所示:
过P作PE∥AD交CD于E,
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠β﹣∠α;
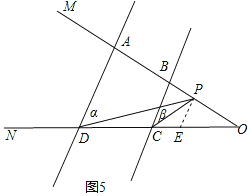
当P在AB延长线时,如图5所示:
同(2)可知:∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠α﹣∠β.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若![]() ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
①<1.493>=1;
②<2x>=2<x>;
③若![]() ,则实数x的取值范围是
,则实数x的取值范围是![]() ;
;
④当x≥0,m为非负整数时,有![]() ;
;
⑤![]() 。
。
其中,正确的结论有 (填写所有正确的序号)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:据统计图解答下列问题: 
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:① GA=GP;② S△PAC∶S△PAB=AC∶AB;③ BP垂直平分CE;④ FP=FC,其中正确的判断有( )
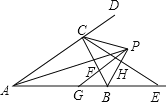
A. 只有①② B. 只有③④ C. 只有①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知A(2,2)、B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌电风扇销售量的情况,对某商场5月份该品牌甲、乙、丙三种型号的电风扇销售量进行统计,绘制如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该商场5月份售出这种品牌的电风扇共多少台?
(2)若该商场计划订购这三种型号的电风扇共2000台,根据5月份销售量的情况,求该商场应订购丙种型号电风扇多少台比较合理?

查看答案和解析>>
科目:初中数学 来源: 题型:
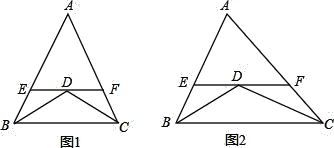
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
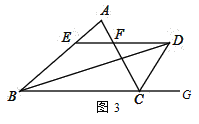
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 图像上一点,作
图像上一点,作![]() 轴于点
轴于点![]() ,且
,且![]() 的面积为
的面积为![]() ,点
,点![]() 坐标为
坐标为![]() .
.

(![]() )求
)求![]() 和
和![]() 的值.
的值.
(![]() )若直线
)若直线![]() 经过点
经过点![]() ,交另一支双曲线于点
,交另一支双曲线于点![]() ,求
,求![]() 的面积.
的面积.
(![]() )指出
)指出![]() 取何值时,一次函数的值大于反比例函数的值,直接写出结果.
取何值时,一次函数的值大于反比例函数的值,直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com