
 如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.
如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据BC=2AB,H为BC中点,可得△ABH为等腰直角三角形,HE=BH=HC,可得△CEH为等腰三角形,又∠BCD=90°,CE⊥BD,利用互余关系得出角的相等关系,根据基本图形判断全等三角形,特殊三角形进行判断.
解答 解:①在△BCE中,∵CE⊥BD,H为BC中点,
∴BC=2EH,又BC=2AB,
∴EH=AB,①正确;
②由①可知,BH=HE∴∠EBH=∠BEH,
又∠ABG+∠EBH=∠BEH+∠HEC=90°,
∴∠ABG=∠HEC,②正确;
③由AB=BH,∠ABH=90°,得∠BAG=45°,
同理:∠DHC=45°,∴∠EHC>∠DHC=45°,
∴△ABG≌△HEC,③错误;
④作AM⊥BD,则AM=CE,△AMD≌△CEB,
∵AD∥BC,
∴△ADG∽△HGB,
∴$\frac{AG}{GH}$=2,
即△ABG的面积等于△BGH的面积的2倍,
根据已知不能推出△AMG的面积等于△ABG的面积的一半,
即S△GAD≠S四边形GHCE,
∴④错误
⑤∠ECH=∠CHF+∠F=45°+∠F,
又∠ECH=∠CDE=∠BAO,∠BAO=∠BAH+∠HAC,
∴∠F=∠HAC,
∴CF=BD,⑤正确.
正确的有3个.
故选C.
点评 此题主要考查了等腰三角形的判定与性质、矩形的判定与性质、全等三角形的判定与性质、相似三角形的判定.解答该题的关键是证明等腰三角形,全等三角形.本题综合性较强,难度比较大.


科目:初中数学 来源: 题型:解答题
 某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
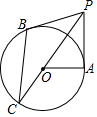 如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )
甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示,则乙比甲每小时快( )| A. | 20km/h | B. | 30km/h | C. | 40km/h | D. | 50km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150名 | B. | 300名 | C. | 600名 | D. | 900名 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com