
【题目】如图,已知在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,对角线OC、AB交于点D,点E、F、G分别是CD、BD、BC的中点,以O为原点,直线OB为x轴建立平面直角坐标系,则G、E、D、F四个点中与点A在同一反比例函数图象上的是( )

A. 点G B. 点E C. 点D D. 点F
【答案】A
【解析】如下图,过点D作DM⊥OB于点M,则∠OME=90°,
∵在直角梯形AOBC中,AC∥OB,CB⊥OB,OB=18,BC=12,AC=9,
∴点A的坐标为(9,12),点B的坐标为(18,0),点C的坐标为(18,12),∠OBC=90°=∠ACB,△ACD∽△BDO,△OMD∽△OBC,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴DM=8,OM=12,
∴点D的坐标为(12,8),
∵点点E、F、G分别是CD、BD、BC的中点,
∴点E、F、G的坐标分别为(15,10)、(15,4)、(18,6),
∵在点A(9,12)中,9×12=108;点E(15,10)中,15×10=150;点F(15,4)中,15×4=60;点G(18,6)中18×6=1-8;
∴点A和点G中同一反比例函数的图象上.
故选A.



科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边 ABC 的边长是 2 , D 、 E 分别为 AB 、 AC 的中点,连接CD ,过 E 点作 EF // DC 交 BC 的延长线于点 F
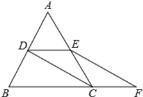
(1) 求证:四边形 CDEF 是平行四边形;
(2)求四边形 CDEF 的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
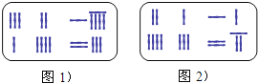
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月29日至2019年10月7日,2019年中国北京世界园艺博览会(简称北京世园会)在中国北京市延庆区举行,展期162天.这是继云南昆明后第二个获得国际园艺生产者协会批准及国际展览局认证授权举办的A1级国际园艺博览会.北京世园会门票种类分为平日票、指定日票、三次票等票种,同时按销售对象分为普通票、优惠票和团队票(学生享受优惠票,15人以上可以享受团体票).指定日包括开园日、“五一”假期、端午节假期、中秋节假期、“十一”假期这些日期,其余时间为平日;三次票是指除指定日外,同一持票人在展会期间可以任选三天入园的票种. 具体如下表:
平日票价(元/张) | 指定日票价(元/张) | 三次票(元/张) | |
普通票 | 120 | 160 | 300 |
优惠票 | 80 | 100 |
小明,小亮两家共10人打算一起参观北京世园会(10人均需购票).
(1)若他们端午节去北京世园会参观购买门票共用去1360元,问买了普通票和优惠票各几张?
(2)如果他们平日去北京世园会参观,且购买门票的费用不超过2000元,那么在保证游玩的前提下最多可以买几张三次票?共有几种买票方案?分别是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B =∠C,点D、E分别是边AB、AC上的点,PD平分∠BDE交BC于H,PE平分∠DEC交BC于G,DQ平分∠ADE交PE延长线于Q。

(1)∠A+∠B+∠C+∠P +∠Q = °;
(2)猜想∠P与∠A的数量关系,并证明你的猜想;
(3)若∠EGH =112°,求∠ADQ 的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④4a﹣2b+c<0;⑤c﹣a>1.其中所有正确结论的序号是_____.
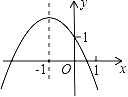
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G。
DC,连接EF并延长交BC的延长线于点G。
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com