
已知二次函数 , 在
, 在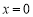 和
和 时的函数值相等.
时的函数值相等.
(1)求二次函数的解析式;
(2)若一次函数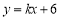 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点 ,求
,求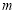 和
和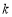 的值;
的值;
(3)设二次函数的图象与 轴交于点
轴交于点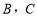 (点
(点 在点
在点 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点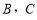 间的部分(含点
间的部分(含点 和点
和点 )向左平移
)向左平移 个单位后得到的图象记为
个单位后得到的图象记为 ,同时将(2)中得到的直线
,同时将(2)中得到的直线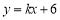 向右平移
向右平移 个单位.请结合图象回答:当平移后的直线与图象
个单位.请结合图象回答:当平移后的直线与图象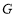 有公共点时,
有公共点时, 的取值范围.
的取值范围.
【解析】
(1)∵二次函数y=(t+1)x2+2(t+2)x+
在x=0和x=2时的函数值相等,
∴对称轴x=-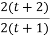 =1
=1
即-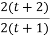 =1
=1
解得,t=-
则二次函数的解析式为:y=(- +1)x2+2(-
+1)x2+2(- +2)x+-
+2)x+-
即y=- (x+1)(x-3)或y=-
(x+1)(x-3)或y=- (x-1)2+2,
(x-1)2+2,
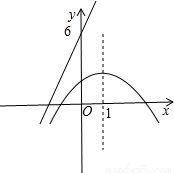
∴该函数图象的开口方向向下,且经过点(-1,0),(3,0),(0, ),顶点坐标是(1,2).其图象如图所示:
),顶点坐标是(1,2).其图象如图所示: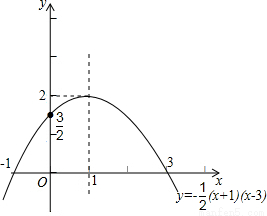
(2)∵二次函数的象经过点A(-3,m),
∴m=- (-3+1)(-3-3)=-6.
(-3+1)(-3-3)=-6.
又∵一次函数y=kx+6的图象经过点A(-3,m),
∴m=-3k+6,即-6=-3k+6,
解得,k=4.
综上所述,m和k的值分别是-6、4.
(3)【解析】
由题意可知,点B、C间的部分图象的解析式是y=- x2+x+
x2+x+ =--
=-- (x2-2x-3)=--
(x2-2x-3)=-- (x-3)(x+1),-1≤x≤3,
(x-3)(x+1),-1≤x≤3,
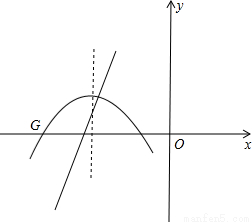
则抛物线平移后得出的图象G的解析式是y=- (x-3+n)(x+1+n),-n-1≤x≤3-n,
(x-3+n)(x+1+n),-n-1≤x≤3-n,
此时直线平移后的解析式是y=4x+6+n,
如果平移后的直线与平移后的二次函数相切,
则方程4x+6+n=- (x-3+n)(x+1+n)有两个相等的实数解,
(x-3+n)(x+1+n)有两个相等的实数解,
即-- x2-(n+3)x-
x2-(n+3)x- n2-
n2- =0有两个相等的实数解,
=0有两个相等的实数解,
判别式△=[-(n+3)]2-4×(- )×(-
)×(- n2--
n2-- )=6n=0,
)=6n=0,
即n=0,
∵与已知n>0相矛盾,
∴平移后的直线与平移后的抛物线不相切,
∴结合图象可知,如果平移后的直线与抛物线有公共点,
则两个临界的交点为(-n-1,0),(3-n,0),
则0=4(-n-1)+6+n,
n= ,0=4(3-n)+6+n,
,0=4(3-n)+6+n,
n=6,
即n的取值范围是: ≤n≤6
≤n≤6
【解析】
试题分析:(1)根据已知条件知,该函数的对称轴方程为x=1,则-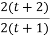 =1,据此易求t的值,
=1,据此易求t的值,
把t的值代入函数解析式即可;根据图象与坐标轴的交点坐标,顶点坐标画出图象;
(2)把点A的坐标代入二次函数解析式,利用方程可以求得m的值;然后把点A的坐标代入一次
函数解析式,也是利用方程来求k的值.
(3)求出点B、C间的部分图象的解析式是y=-(x-3+n)(x+1+n),-n-1≤x≤3-n,直线平移
后的解析式是y=4x+6+n,若两图象有一个交点时,得出方程4x+6+n=-  (x-3+n)(x+1+n)有
(x-3+n)(x+1+n)有
两个相等的实数解,求出判别式△=6n=0,求出的n的值与已知n>0相矛盾,得出平移后
的直线与抛物线有两个公共点,设两个临界的交点为(-n-1,0),(3-n,0),代入直
线的解析式,求出n的值,即可得出答案.
考点:用待定系数法求二次函数解析式,二次函数的性质,二次函数图像上点的特点


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年福建省龙岩市分校九年级上学期第三次阶段考试数学试卷(解析版) 题型:解答题
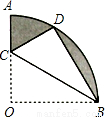
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省福安市小片区九年级上学期半期考试数学试卷(解析版) 题型:选择题
矩形、菱形、正方形都具有的性质是( )
A.每一条对角线平分一组对角
B.对角线相等
C.对角线互相平分
D.对角线互相垂直
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:填空题
在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.设坐标轴的单位长度为1cm,整点P从原点O出发,作向上或向右运动,速度为1cm/s.当整点P从原点出发1秒时,可到达整点(1,0)或(0,1);当整点P从原点出发2秒时,可到达整点(2,0)、(0,2)或 ;当整点P从原点出发4秒时,可以得到的整点的个数为 个.当整点P从原点出发n秒时,可到达整点(x,y),则x、y和n的关系为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市平谷区九年级上学期期末考试数学试卷(解析版) 题型:选择题
在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号为偶数的概率为
A.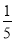 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若以每箱50元价格出售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市九年级上学期期中检测数学试卷(解析版) 题型:解答题
已 知抛物线
知抛物线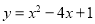 .
.
(1)用配方法将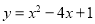 化成
化成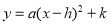 的形式;
的形式;
(2)将此抛物线向右平移1个单位,再向上平移2个单位,求平移后所得抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省淮北市五校九年级上学期第三次联考数学试卷(解析版) 题型:解答题
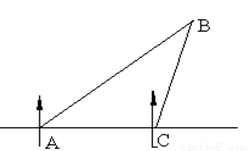
一船在A处测得北偏东60°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北沙河二十冶第3中学八年级上学期主科抽测数学卷(解析版) 题型:选择题
估计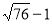 的大小在( )
的大小在( )
A.5--6之间 B.6--7之间 C.7--8之间 D.8--9之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com