
【题目】边长为1的正方形OA![]() B
B![]() C
C![]() 的顶点A
的顶点A![]() 在X轴的正半轴上,如图将正方形OA
在X轴的正半轴上,如图将正方形OA![]() B
B![]() C
C![]() 绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图像上,
则a的值为___________.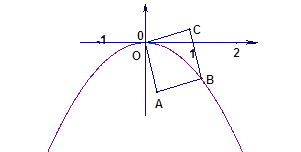
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=5,AC=![]() ,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )
,CB的反向延长线上有一动点D,以AD为边在右侧作等边三角形,连CE,CE最短长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC与直角三角形BDE中,点B,C,D在同一条直线上,已知AC=AE=CD,∠BAC和∠ACB的角平分线交于点F,连DF,EF,分别交AB、BC于M、N,已知点F到△ABC三边距离为3,则△BMN的周长为____________.
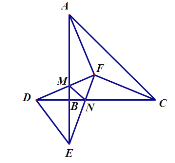
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用大小相同高度为2cm的10块小长方体垒了两堵与地面垂直的木墙AD, BE,当他将一个等腰直角三角板ABC如图垂直放入时,直角顶点C正好在水平线DE上,锐角顶点A和B分别与木墙的顶端重合,求两堵木墙之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》,其主要突破在“五边形数”的证明上.如图为前几个“五边形数”的对应图形,请据此推断,第10个“五边形数”应该为( ),第2018个“五边形数”的奇偶性为( )

A. 145;偶数 B. 145;奇数 C. 176;偶数 D. 176;奇数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com