
【题目】如图①,点G是等边三角形AOB的外心,点A在第一象限,点B坐标为(4,0),连结OG.抛物线y=ax(x﹣2)+1+![]() 的顶点为P.
的顶点为P.
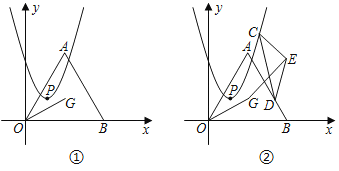
(1)直接写出点A的坐标与抛物线的对称轴;
(2)连结OP,求当∠AOG=2∠AOP时a的值.
(3)如图②,若抛物线开口向上,点C,D分别为抛物线和线段AB上的动点,以CD为底边构造顶角为120°的等腰三角形CDE(点C,D,E成逆时针顺序),连结GE.
①点Q在x轴上,当四边形GDQO为平行四边形时,求GQ的值;
②当GE的最小值为1时,求抛物线的解析式.
【答案】(1)A(2,2![]() ),1;(2)﹣1或
),1;(2)﹣1或![]() ;(3)①
;(3)①![]() ;②y=(x﹣1)2+
;②y=(x﹣1)2+![]()
【解析】
(1)由等边三角形的性质可求点A坐标,由抛物线的性质可求对称轴;
(2)分两种情况讨论,由直角三角形的性质可求点P坐标,代入解析式可求a的值;
(3)①连接AG并延长AG交OB于H,由等边三角形外心的性质可求GH的长,由平行四边形的性质可得GD∥OB,GD=OQ,由平行线分线段成比例可求GD的长,由勾股定理可求解;
②在OB上截取OM=BD,连接CM,GM,GB,MD,GD,通过证明△GDE∽△MDC,可得![]() =
=![]() ,则当GE最小值为1时,MC最小值为
,则当GE最小值为1时,MC最小值为![]() ,可得当点C与抛物线顶点P重合,且CM⊥OB时,CM有最小值,即可求点P坐标,代入解析式可求解.
,可得当点C与抛物线顶点P重合,且CM⊥OB时,CM有最小值,即可求点P坐标,代入解析式可求解.
解:(1)如图,连接AG并延长AG交OB于H,
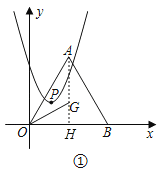
∵点B坐标为(4,0),
∴OB=4,
∵点G是等边三角形AOB的外心,
∴AH⊥OB,OA=OB=4,∠AOB=60°,
∴∠OAH=30°,
∴OH=![]() OA=2,AH=
OA=2,AH=![]() OH=2
OH=2![]() ,
,
∴点A(2,2![]() ),
),
∵抛物线y=ax(x﹣2)+1+![]() =ax2﹣2ax+1+
=ax2﹣2ax+1+![]() ,
,
∴对称轴为:直线x=﹣![]() =1;
=1;
(2)如图,过点P作PN⊥OB于N,交AO于F,
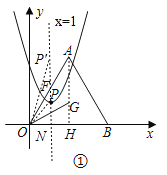
∴ON=1,
∵点G是等边三角形AOB的外心,
∴OG平分∠AOB,
∴∠AOG=30°=∠BOG,
当点P在△AOB内,
∵∠AOG=2∠AOP,
∴∠AOP=15°=∠POG,
∴∠PON=45°,
∵PN⊥OB,
∴∠PON=∠OPN=45°,
∴PN=ON=1,
∴点P坐标(1,1),
∴1=a(1﹣2)+1+![]() ,
,
∴a=![]() ,
,
当点P在△AOB外,
同理可得∠AOP'=15°,
∴∠P'ON=75°,
∴∠OP'N=15°=∠AOP',
∴OF=P'F,
∵∠AOB=60°,P'N⊥OB,
∴OF=2ON=2=P'F,FN=![]() ON=
ON=![]() ,
,
∴P'N=P'F+FN=2+![]() ,
,
∴点P坐标为(1,2+![]() ),
),
∴2+![]() =a(1﹣2)+1+
=a(1﹣2)+1+![]() ,
,
∴a=﹣1,
综上所述:a=﹣1或![]() ;
;
(3)如图,连接AG并延长AG交OB于H,

∵点G是等边三角形AOB的外心,
∴AG=2GH,OH=BH=2,AH=2![]() ,
,
∴GH=![]() ,
,
∵四边形GDQO为平行四边形,
∴GD∥OB,GD=OQ,
∴![]() ,
,
∴GD=![]() ,
,
∴QH=![]() ,
,
∴GQ=![]() =
=![]() =
=![]() ;
;
②如图,在OB上截取OM=BD,连接CM,GM,GB,MD,GD,
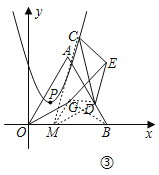
∵点G是等边三角形AOB的外心,
∴OG=GB,∠GOB=∠GBO=∠ABG=30°,
又∵OM=BD,
∴△OGM≌△BGD(SAS),
∴MG=GD,∠OGM=∠BGD,
∴∠OGB=∠MGD=180°﹣30°﹣30°=120°,
∴MD=![]() GD,∠GDM=30°,
GD,∠GDM=30°,
∵△CDE中CE=DE,∠CED=120°,
∴CD=![]() DE,∠CDE=30°,
DE,∠CDE=30°,
∴∠MDC=∠GDE,![]() ,
,
∴△GDE∽△MDC,
∴![]() =
=![]() ,
,
当GE最小值为1时,MC最小值为![]() ,
,
∴当点C与抛物线顶点P重合,且CM⊥OB时,CM有最小值,
∴CM的最小值为顶点P的纵坐标,
∴点P坐标(1,![]() ),
),
∴![]() =a(1﹣2)+1+
=a(1﹣2)+1+![]() ,
,
∴a=1,
∴抛物线的解析式为:y=x(x﹣2)+1+![]() =(x﹣1)2+
=(x﹣1)2+![]() .
.
【点题】
考查了二次函数的性质、全等三角形的判定和性质、相似三角形的判定和性质、等边三角形的性质和垂线段最短等知识,解题关键是添加恰当辅助线构造全等三角形或相似三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
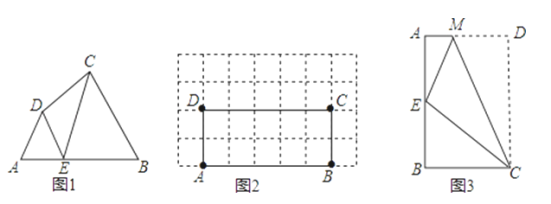
【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”:如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
(1)如图1,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
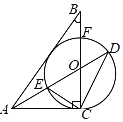
【题目】如图,在△ABC中,∠ACB=90°,AO平分∠BAC,交BC于点O.以O为圆心,OC为半径作⊙O,分别交AO,BC于点E,F.
(1)求证:AB是⊙O的切线;
(2)延长AO交⊙O于点D,连接CD,若AD=2AC,求tanD的值;
(3)在(2)的条件下,设⊙O的半径为3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中为加强学生体质,开展了足球,排球、篮球三门拓展性课程以供学生选择,每位学生必须在三项中选择一项进行报名;选课结束后,将八年级学生选课结果绘制成了如下所示的两个统计图(部分信息未给出),已知该校八年级男生人数比女生多15人,女生选择排球人数是男生选择排球人数的3倍.

(1)求该校八年级女生人数.
(2)补全条形统计图.
(3)小甬经过计算,发现八年级学生选择足球的人数占八年级学生总人数的三分之一.小甬就认为全校有三分之一的学生选报了足球.你认为小甬的想法合理吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
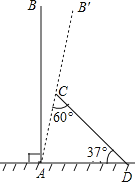
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
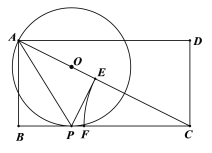
【题目】如图,在矩形ABCD中,CD=2,AD=4,点P在BC上,将△ABP沿AP折叠,点B恰好落在对角线AC上的E点.O为AC上一点,⊙O经过点A,P.
(1)求证:BC是⊙O的切线;
(2)在边CB上截取CF=CE,点F是线段BC的黄金分割点吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】

A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com