
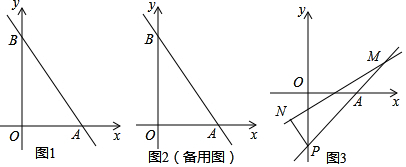
分析 (1)设直线AB的解析式是y=kx+b,代入得到方程组,求出即可;
(2)当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,证△BMN≌△ABO(AAS),求出M的坐标即可;②当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,同法求出M的坐标;③当AM⊥BM,且AM=BM时,过M作MN⊥x轴于N,MH⊥y轴于H,证△BHM≌△AMN,求出M的坐标即可.
(3)设NM与x轴的交点为H,分别过M、H作x轴的垂线垂足为G,HD交MP于D点,求出H、G的坐标,证△AMG≌△ADH,△AMG≌△ADH≌△DPC≌△NPC,推出PN=PD=AD=AM代入即可求出答案.
解答 解:(1)∵A(2,0),B(0,4),
设直线AB的解析式是y=kx+b,
代入得:$\left\{\begin{array}{l}{2k+b=0}\\{b=4}\end{array}\right.$,
解得:k=-2,b=4,
∴直线AB的解析式是y=-2x+4.
(2)分三种情况:
①如图1,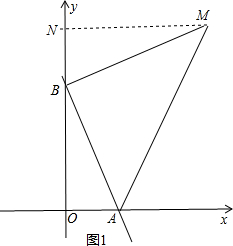
当BM⊥BA,且BM=BA时,过M作MN⊥y轴于N,
∵BM⊥BA,MN⊥y轴,OB⊥OA,
∴∠MBA=∠MNB=∠BOA=90°,
∴∠NBM+∠NMB=90°,∠ABO+∠NBM=90°,
∴∠ABO=∠NMB,
在△BMN和△ABO中$\left\{\begin{array}{l}{∠MNB=∠BOA}\\{∠NMB=∠ABO}\\{BM=AB}\end{array}\right.$,
∴△BMN≌△ABO(AAS),
MN=OB=4,BN=OA=2,
∴ON=2+4=6,
∴M的坐标为(4,6 ),
代入y=mx得:m=$\frac{3}{2}$,
②如图2,
当AM⊥BA,且AM=BA时,过M作MN⊥x轴于N,
易知△BOA≌△ANM(AAS),
同理求出M的坐标为(6,2),
代入y=mx得:m=$\frac{1}{3}$,
③如图4,
当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,
∴四边形ONMH为矩形,
易知△BHM≌△AMN,
∴MN=MH,
设M(x1,x1)代入y=mx得:x1=m x1,
∴m=1,
答:m的值是$\frac{3}{2}$或$\frac{1}{3}$或1.
(3)解:如图,
设NM与x轴的交点为H,过M作MG⊥x轴于G,过H作HD⊥x轴,
HD交MP于D点,
即:∠MGA=∠DHA=90°,连接ND,ND 交y轴于C点
由y=$\frac{k}{2}$x-$\frac{k}{2}$与x轴交于H点,
∴H(1,0),
由y=$\frac{k}{2}$x-$\frac{k}{2}$与y=kx-2k交于M点,
∴M(3,k),
而A(2,0),
∴A为HG的中点,AG=AH,∠MAG=∠DAH
∴△AMG≌△ADH(ASA),
∴AM=AD
又因为N点的横坐标为-1,且在y=$\frac{k}{2}$x-$\frac{k}{2}$上,
∴N(-1,-k),
同理:D(1,-k),P(0,-2k),
∴N关于y轴对称点为D,
∴PC是ND的垂直平分线,
∴PN=PD,ND平行于X轴,
易知△ADH≌△DPC,
∴AD=PD,
∴PN=PD=AD=AM,
∴$\frac{PM-PN}{AM}$=$\frac{3AM-AM}{AM}$=2.
点评 此题是一次函数综合题,主要考查对一次函数图象上点的坐标特征,等腰直角三角形性质,用待定系数法求正比例函数的解析式,全等三角形的性质和判定,二次根式的性质等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
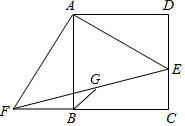 E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( )
E为正方形ABCD的边CD上一点,将△ADE绕A点顺时针旋转90°,得△ABF,G为EF中点.下列结论:①G在△ABF的外接圆上;②EC=$\sqrt{2}$BG;③B,G,D三点在同一条直线上;④若S四边形BGEC=$\frac{1}{4}$S正方形ABCD,那么E为DC的黄金分割点.正确的是( )| A. | ①② | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
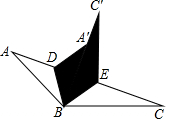 如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.
如图所示,将一张三角形纸片分别沿着BD,BE对折,使点C落在点C′,点A落在点A′,点B,A′,C′在同一条直线上,若∠ABC=130°,则∠DBE=65度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.
已知抛物线y=-x2+bx+3交x轴负、正半轴于A、B两点,交y轴与点C,且tan∠ACO=$\frac{1}{3}$,△ABC的外接圆的圆心为M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com