
【题目】如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶5
(1)如图,若∠BOD=70°,求∠BOE
(2)如图,若OF平分∠BOE,∠BOF=∠AOC+10°,求∠EOF

【答案】(1) 160°;(2) 80°
【解析】
(1)根据对顶角相等,可得∠AOC的度数,根据∠AOE:∠EOC=2:5,可得∠AOE,根据邻补角,可得答案;(2)根据角平分线的性质,可得∠BOE,根据∠AOE:∠EOC=2:5,可得∠AOE,根据邻补角的关系,可得关于∠AOC的方程,根据角的和差,可得∠BOE,根据角平分线的性质,可得答案.
解:(1)由对顶角相等,得∠AOC=∠BOD=70°,由OE把∠AOC分成两部分且∠AOE:∠EOC=2:5,得∠AOE=∠AOC×![]() =20°,
=20°,
由邻补角,得∠BOE=180°-∠AOE=180°-20°=160°,
(2)由OF平分∠BOE,得∠BOE=2∠BOF=2∠AOC+20°,
由∠AOE:∠EOC=2:5,得∠AOE=![]() ∠AOC,
∠AOC,
由邻补角,得∠BOE+∠AOE=180°,即2∠AOC+20°+![]() ∠AOC=180°.
∠AOC=180°.
解得∠AOC=70°,∠AOE=![]() ∠AOC=
∠AOC=![]() ×70=20°,
×70=20°,
由角的和差,得∠BOE=180°-∠AOE=180°-20°=160°,
由OF平分∠BOE,得∠EOF=![]() ∠BOE=
∠BOE=![]() ×160°=80°.
×160°=80°.


科目:初中数学 来源: 题型:
【题目】如图,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.
(1)在坐标纸上画出这几次变换相应的图形;
(2)设P(x,y)为△OAB边上任一点,依次写出这几次变换后点P对应点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王平同学为小明与小丽设计了一种游戏.游戏规则是:取3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再按原样放回,洗匀后第二次再随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小明胜;若两数字之和为奇数,则小丽胜.问这种游戏规则公平吗?请通过画树状图或列表说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
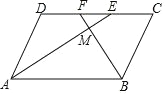
【题目】如图,在 ABCD 中,AE、BF 分别平分∠DAB 和∠ABC,交 CD 于点 E、F,AE、BF 相交于点 M.
(1)求证:AE⊥BF;
(2)判断线段 DF 与 CE 的大小关系,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,点D和点B关于直线AC轴对称.点M(不同于点A和点C)在射线CA上,线段DM的垂直平分线交直线BC的于N,
(1)如图,过点D作DE⊥BC,交BC的延长线于E,若CE=5,求BC的长;
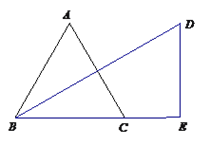
(2)如图,若点M在线段AC上,求证:△DMN为等边三角形;

(3)连接CD,BM,若![]() ,直接写出
,直接写出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-2amx+am2+2m+4的顶点P在一条定直线l上.
(1)直接写出直线l的解析式;
(2)若存在唯一的实数m,使抛物线经过原点.
①求此时的a和m的值;
②抛物线的对称轴与x轴交于点A,B为抛物线上一动点,以OA、OB为边作□OACB,若点C在抛物线上,求B的坐标.
(3)抛物线与直线l的另一个交点Q,若a=1,直接写出△OPQ的面积的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,补充下列结论和依据.

∵∠ACE=∠D(已知),
∴_____∥______(______________________ ).
∵∠ACE=∠FEC(已知),
∴______∥______(_ ___ _______).
∵∠AEC=∠BOC(已知),
∴_____∥______(___ _____________________).
∵∠BFD+∠FOC=180°(已知),
∴_____∥______(_____ ____________________).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com