
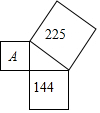
 如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.
如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为81.  导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
 如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.
如图一架云梯AB斜靠在一面墙上,梯子的底端B离墙根O的距离OB长为7米,梯子的顶端A到地面的距离OA为24米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
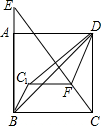 如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.
如图,在边长为5的正方形ABCD中,E是线段BA延长线上一点,且AE=$\frac{1}{3}$AB,连接CE,在线段CE上取一点F,使得CF=$\frac{5}{2}$,连接FD,将△CFD沿FD折叠至△C1FD,连接C1B,则△C1BD的面积为$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线a与c的夹角是∠α,直线b与c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α+∠β=180°时,直线a∥b,理由是同旁内角互补,两直线平行.
如图,直线a与c的夹角是∠α,直线b与c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足∠α+∠β=180°时,直线a∥b,理由是同旁内角互补,两直线平行.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?
用长32米的篱笆围成面积为130m2的矩形场地,矩形场地的一面利用墙可用最大长度为16m,与墙平行的对边有1m长的一道门,求此矩形场地的长、宽各是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com