
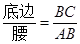 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. 根据上述关于角的正对定义,解决下列问题: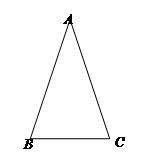
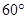 的值为( ▲ )
的值为( ▲ )A.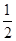 | B.1 | C.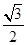 | D.2 |
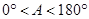 ,∠A的正对值sadA的取值范围是( ▲ )
,∠A的正对值sadA的取值范围是( ▲ )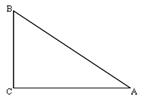
A.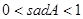 | B. | C.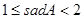 |
D.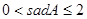 |
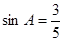 ,AB=25试求sadA的值
,AB=25试求sadA的值 =1.
=1.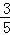 .
.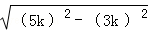 =4k,
=4k,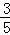 .
. k,AH=
k,AH=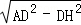 =
=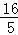 k.
k.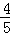 k,CD=
k,CD=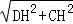 =
=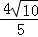 k.
k.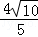 k.
k. =
=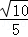 ,即sadα=
,即sadα=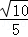 .(12分)
.(12分)


科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
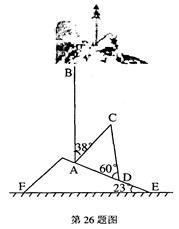
 分别表示甲、乙两建筑物的高,
分别表示甲、乙两建筑物的高, ,从
,从 点测得
点测得 点的仰角
点的仰角 为60°从
为60°从 点测得
点测得 点的仰角
点的仰角 为30°,已知甲建筑物高
为30°,已知甲建筑物高 米.
米.
 ;
; (结果精确到0.01米).
(结果精确到0.01米). )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com