
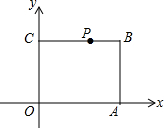
 在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y=$\frac{k}{x}$上,则k值可以是10或12或8.
在平面直角坐标系中,点A的坐标为(5,0),点C的坐标为(0,4),四边形ABCO为矩形,点P为线段BC上的一动点,若△POA为等腰三角形,且点P在双曲线y=$\frac{k}{x}$上,则k值可以是10或12或8. 分析 当PA=PO时,根据P在OA的垂直平分线上,得到P的坐标;当OP=OA=5时,由勾股定理求出CP即可;当AP=AO=5时,同理求出BP、CP,即可得出P的坐标,然后把P的坐标代入线y=$\frac{k}{x}$,即可求得k的值.
解答 解:∵点A的坐标为(5,0),点C的坐标为(0,4),
∴当PA=PO时,P在OA的垂直平分线上,P的坐标是(2.5,4);
当OP=OA=5时,由勾股定理得:CP=$\sqrt{O{P}^{2}-C{P}^{2}}$=3,P的坐标是(3,4);
当AP=AO=5时,同理BP=3,CP=5-3=2,P的坐标是(2,4).
∵点P在双曲线y=$\frac{k}{x}$上,
∴k=2.5×4=10或k=3×4=12或k=2×4=8,
故答案为10或12或8.
点评 本题主要考查对矩形的性质,等腰三角形的性质,勾股定理以及反比例图象上点点坐标特征等知识点的理解和掌握,能求出所有符合条件的P的坐标是解此题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )
如图,分别以边长等于2的正方形的四边为直径作半圆,则圆中阴影部分的面积为( )| A. | $\frac{π}{2}$-1 | B. | 2π-2 | C. | π+1 | D. | 2π-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 移植的棵数n | 300 | 700 | 1000 | 5000 | 15000 |
| 成活的棵数m | 280 | 622 | 912 | 4475 | 13545 |
| 成活的频率$\frac{m}{n}$ | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
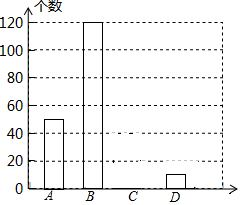 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:| 关注情况 | 频数 | 频率 |
| A.高度关注 | 50 | b |
| B.一般关注 | 120 | 0.6 |
| C.不关注 | a | 0.1 |
| D.不知道 | 10 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
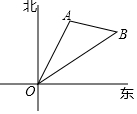 如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)
如图,海岛A在灯塔O处北偏东25°,海岛B在灯塔O处北偏东55°,海岛A在海岛B的北偏西80°,已知海岛A到灯塔的距离为80海里,求海岛B到灯塔的距离.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
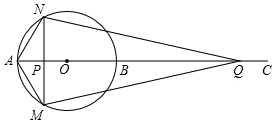 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com