
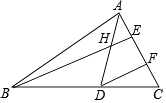
【题目】如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
求∠FDC和∠AHB的度数.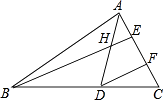
【答案】解:∵BE⊥AC,
∴∠BEC=90°,
∵DF∥BE,
∴∠BEC=∠DFC=90°,
∵∠C=64°,
∴∠FDC=180°﹣(∠DFC+∠C)
=180°﹣(90°+64°)
=26°,
∵∠ABC=36°,∠C=64°,
∴∠BAC=180°﹣∠ABC﹣∠C=180°﹣36°﹣64°=80°,
∵AD平分∠BAC,
∴∠DAC= ![]() ∠BAC=
∠BAC= ![]() ×80°=40°,
×80°=40°,
∴∠AHB=∠DAC+∠BEA
=40°+90°
=130°.
【解析】先根据平行线的性质求出∠C=64°,再根据三角形的内角和定理即可求出结论.
【考点精析】根据题目的已知条件,利用平行线的性质和三角形的内角和外角的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.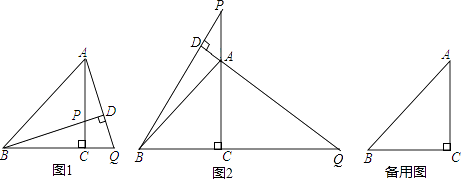
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立?(填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA=度时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是 ;
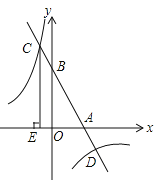
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数![]() 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若![]() ,则b的值是 .
,则b的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
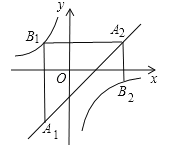
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若![]() ,则a2015= .
,则a2015= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: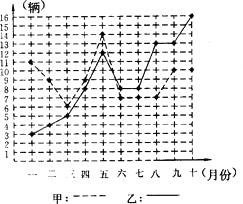
(1)请你根据上图填写下表.
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:①从平均数和方差结合看;②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育馆计划从一家体育用品商品一次性购买若干个排球和篮球(每个排球的价格都相同,每个篮球的价格都相同),双方洽谈的信息如下:
信息一:购买1个排球和2个篮球共需210元;
信息二:购买2个排球和3个篮球共需340元;
信息三:购买排球和篮球共50个,总费用不超过3200元,且购买排球的个数少于30个.
(1)每个排球和每个篮球的价格各是多少元?
(2)该体育馆有几种购买方案?应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com