
分析 先把点代入y=(x-1)2-k可得k=4,则得到抛物线解析式为y=x2-2x-3,再解方程x-1)2-4=0B(3,0),设C(t,t2-2t-3),利用三角形面积公式得到$\frac{1}{2}$•(3+1)•|t2-2t-3|=8,然后解关于t的绝对值方程即可得到C点坐标.
解答 解:把A(-1,0)代入y=(x-1)2-k得4-k=0,解得k=4,
所以抛物线解析式为y=(x-1)2-4,即y=x2-2x-3,
当y=0时,(x-1)2-4=0,解得x1=-1,x2=3,则B(3,0),
设C(t,t2-2t-3),
因为S△ABC=8,
所以$\frac{1}{2}$•(3+1)•|t2-2t-3|=8,
当t2-2t-3=4,解得t1=1+2$\sqrt{2}$,t2=1-2$\sqrt{2}$,此时C点坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4),
当t2-2t-3=-4,解得t1=t2=1,此时C点坐标为(1,-4),
综上所述,点C的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程ax2+bx+c=0.也考查了三角形面积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).
如图,圆柱形容器中,高为18cm,底面周长为24cm,在容器内壁离容器底部4cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为0.2m(容器厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)
如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(-3,0),C(0,-3)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
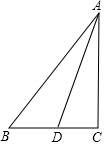 如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.
如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com