
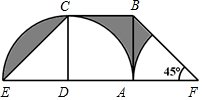
 如图,ABCD是一个正方形,ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14)
如图,ABCD是一个正方形,ED=DA=AF=2厘米,阴影部分的面积是多少平方厘米?(π取3.14) 分析 根据正方形的性质得到AD=CD=BC=AB,推出△CDE与△ABF是等腰直角三角形,根据扇形和三角形的面积公式即可得到结论.
解答 解:∵四边形ABCD是一个正方形,
∴AD=CD=BC=AB,
∵ED=DA=AF=2厘米,
∴△CDE与△ABF是等腰直角三角形,
∴阴影部分的面积=$\frac{1}{2}$S正方形ABCD+$\frac{1}{2}$△ABF-S扇形=$\frac{1}{2}×$2×2+$\frac{1}{2}$×2×2-$\frac{45•π×{2}^{2}}{360}$=4-$\frac{π}{2}$=2.43平方厘米.
点评 本题考查了扇形的面积的计算,三角形的面积的计算,正方形的性质,正确的识别图形是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com