
����Ŀ������������֪��l��m��n��k��ƽ����l��m��m��n��n��k֮��ľ���ֱ�Ϊd1��d2��d3����d1��d3��1��d2��2.���ǰ��ĸ�����ֱ���l��m��n��k������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ� ��
��̽��1��(1)��ͼ1��������ABCDΪ�������ı��Ρ���BE��l�ڵ�E��BE�ķ����ӳ��߽�ֱ��k�ڵ�F.��������ABCD�ı߳���
��̽��2��(2)��ͼ2������ABCDΪ�������ı��Ρ��ҡ�ADC��60�㣬��AEF�ǵȱ������Σ�AE��k�ڵ�E����AFD��90�㣬ֱ��DF�ֱ�ֱ��l��k�ڵ�G����M.��֤��EC��DF��
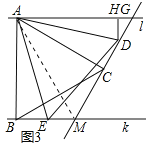
����չ��(3)��ͼ3��l��k���ȱߡ�ABC�Ķ���A��B�ֱ�����ֱ��l��k�ϣ�AB��k�ڵ�B���ҡ�ACD��90�㣬ֱ��CD�ֱ�ֱ��l��k�ڵ�G����M����D����E�ֱ����߶�GM��BM�ϵĶ��㣬��ʼ�ձ���AD��AE��DH��l�ڵ�H.���룺DH��ʲô��Χ�ڣ�BC��DE����˵����ʱBC��DE�����ɣ�

���𰸡���1��![]() ����2��֤������������3����2��DH��4ʱ��BC��DE�����ɼ�����.
����2��֤������������3����2��DH��4ʱ��BC��DE�����ɼ�����.
����������1��֤����ABE�ա�BCF���������AE�ij���Ȼ�����ù��ɶ���������⣻
��2����B��BE��l�ڵ�E����k�ڵ�F����֤��AEB�ס�BCF��Ȼ���AB�dz���AB�ǿ������������������ã�
��3������AC��֤��ֱ�ǡ�AEC��ֱ�ǡ�AFD����֤�ã�
��4������֤��AM��BC��Ȼ��֤��Rt��ABE��Rt��ACD���õ���BAE=��CAD����AM��ED������֤��BC��DE��
��1���⣺��l��k��BE��l��
���BFC=��BEA=90�㣬
���ABE+��BAE=90�㣬
���ı���ABCD�������Σ�
���ABC=90�㣬AB=BC��
���ABE+��CBF=90�㣬
���BAE=��CBF��
�ڡ�ABE�͡�BCF�У���BEA=��CFB����BAE=��CBF��AB=BC
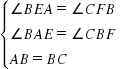
�����ABE�ա�BCF��AAS����
��AE=BF��
��d1=d3=1��d2=2��
��BE=3��AE=1��
��ֱ�ǡ�ABE�У�AB=![]() =
=![]() =
=![]() ��
��
�������εı߳���![]() ��
��
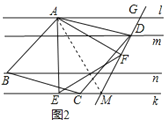
��2��֤��������AC����ͼ2��ʾ��
���ı���ABCD�����Σ��ҡ�ADC=60�㣬
��AC=AD��
�ߡ�AEF�ǵȱ������Σ�
��AE=AF��
��AE��k����AFD=90�㣬
���AEC=��AFD=90�㣬
��Rt��AEC��Rt��AFD��AC=AD��AE=AF��
![]() ��
��
��Rt��AEC��Rt��AFD��HL����
��EC=DF��
��3���⣺��2��DH��4ʱ��BC��DE���������£�
��ͼ3��ʾ����2��DH��4ʱ����D���߶�CM�ϣ�����AM��
���ABM=��ACM=90�㣬AB=AC��AM=AM��
��Rt��ABM��Rt��ACM��AM=AM��AB=AC��
![]() ��
��
��Rt��ABM��Rt��ACM��HL����
���BAM=��CAM��
��AM��BC��
��Rt��ABE��Rt��ACD��AE=AD��AB=AC��
![]() ��
��
��Rt��ABE��Rt��ACD��HL����
���BAE=��CAD��
���EAM=��DAM��
��AM��ED��
��BC��DE��
���㾦�����⿼����ȫ�������ε��ж��������Լ����������ε��ж������ʣ���ȷ�������Ƶ��������ǹؼ�������ʱ����������ȷ���������ߣ�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�죬С��ȥ���Ѽҽ��飬�����Ѽ�ͣ��һ��ʱ����ؼ��У���ͼ������ҵ�·�� ��ǧ�ף���ʱ�� ���֣���ϵ��ͼ����ͼ����Ϣ������˵����ȷ���� ( )
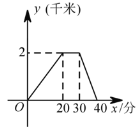
A. С��ȥʱ���ٶȴ��ڻؼҵ��ٶ� B. С��ȥʱ������·���ؼ�ʱ������·
C. С��ȥʱ����ʱ�����ڻؼ�����ʱ�� D. С�������Ѽ�ͣ���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD=![]() AB=
AB= ![]() CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�����axym�ǹ���x��y�ĵ���ʽ����ϵ����4��������5����ôa��m��ֵ�ֱ���________��
(2)�����(a��2)xym�ǹ���x��y����ε���ʽ����ôa��mӦ�����������____________��
(3)�������ʽ2x3y4�룭![]() x2zn�Ĵ�����ͬ����ôn��________.
x2zn�Ĵ�����ͬ����ôn��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y=ax2+bx+c��a��b��cΪ��������a��0�������㣨��1��0������m��0������1��m��2����x����1ʱ��y��x�������С�����н��ۣ� ��abc��0��
��a+b��0��
������A����3��y1����B��3��y2�����������ϣ���y1��y2��
��a��m��1��+b=0��
��c�ܩ�1ʱ����b2��4ac��4a��
���н�����ȷ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=BC=8��AO=BO����M������CO�ϵ�һ�����㣬��AOC=60�㣬��ABMΪֱ��������ʱ��AM�ij�Ϊ____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Լ�õ磬ij�и���ÿ������ÿ���õ�����Ϊ�����շ�.��һ����ۣ�ÿ���õ�������240�ȣ�ÿ��0.4883Ԫ���ڶ�����ۣ�ÿ���õ���Ϊ240~400�ȣ�ÿ��0.5383Ԫ����������ۣ�ÿ���õ���Ϊ������400�ȣ�ÿ��0.7883Ԫ.С��ͬѧ�Ը�����1000�������ijС���������õ�������λ���ȣ������˳������飬��������ͼ��ʾ��ͳ��ͼ.����˵�������������� ��

A. ���γ����������������Ϊ50 B. ���Ƹ�С������һ����۽��ѵľ��������
C. ��С�����ڶ�����۽��ѵľ�����220�� D. ��С������������۽��ѵľ������ԼΪ6%
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������֪��ABC�ǵ��������Σ���BAC=90������D��BC���е㣬��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��1���Բ����߶�BG��AE��������ϵ��
��2����ͼ������������DEFG�Ƶ�D����ʱ�뷽����ת����0�㣼����90�������жϣ�1���еĽ����Ƿ���Ȼ������֤����Ľ��ۣ�

(3)��BC=DE=2,�ڣ�2������ת������,���߶�AE�������ֵ����Сֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊa���������ϼ�ȥһ���߳�Ϊb��С������(a��b)����ʣ�µIJ��ּ�ƴ��һ�����Σ��ֱ����������ͼ����Ӱ���ֵ�������ɴ˿�����֤�ĵ�ʽ��(��)

A. a2��b2��(a��b)(a��b) B. (a��b)2��a2��2ab��b2
C. (a��b)2��a2��2ab��b2 D. a2��ab��a(a��b)
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com