
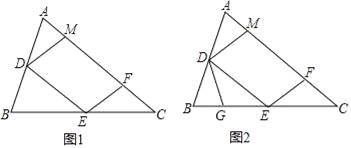
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
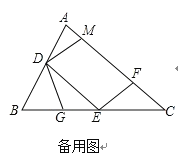
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
【答案】(1)见解析;(2)见解析;(3)EH= 3.
【解析】
(1)根据平行线性质得∠AMD=∠AFE,可证∠AMD=∠A,得DM=DA;(2)根据三角形中位线性质得DE∥AC,证∠DEG=∠C,∠GDE=∠FEC,可证△DEG∽△ECF;(3)证△BDG∽△BED,得![]() ,BD2=BGBE;证△EFH∽△ECF,得
,BD2=BGBE;证△EFH∽△ECF,得![]() ,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
解:(1)证明:如图1所示,
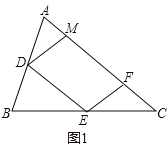
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
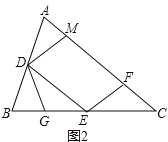
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)如图3所示,
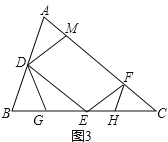
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=3.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.
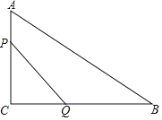
(1)求运动几秒时△PCQ的面积为5cm2?
(2)△PCQ的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由;
(3)是否存在某个时刻t,使四边形ABQP的面积最小?若存在,求出运动时间,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
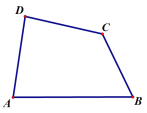
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图,四边形ABCD是“等对角四边形”, ![]() ,则∠C= ;
,则∠C= ;
(2)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=4 , AD=3.求对角线AC的长;
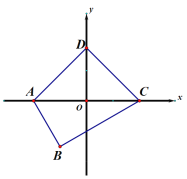
(3)已知:如图,在平面直角坐标系xoy中,四边形ABCD是“等对角四边形”,其中![]() ,点D在y轴上,抛物线
,点D在y轴上,抛物线![]() 过点A、C,点P在抛物线上,当满足
过点A、C,点P在抛物线上,当满足![]() 的P点至少有3个时,总有不等式
的P点至少有3个时,总有不等式![]() 成立,求n 的取值范围.
成立,求n 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y=![]() (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
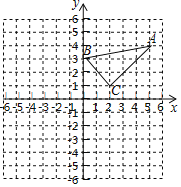
(1)画出△ABC关于原点成中心对称的△A1B1C1,并写出点C1的坐标;
(2)画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
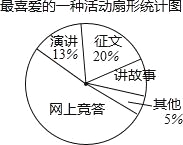
【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式 | 征文 | 讲故事 | 演讲 | 网上竞答 | 其他 |
人数 | 60 | 30 | 39 | a | b |
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B落在AD边上的点M处(点M不与A,D重),点C落在点N处,MN与CD交于点P, 连接MB,当点M在边AD上移动时.有下列结论:①BM=EF;②0<PF<3 ;③∠AMB=∠BMP;④△PDM的周长随之改变.其中正确结论的序号是_______.(把你认为正确的结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
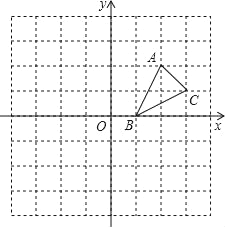
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
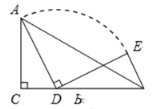
【题目】如图,在△ABC中,∠ACB 90,AC3,CB5,点D是CB边上的一个动点,将线段AD绕着点D 顺时针旋转90,得到线段DE,连结BE,则线段BE的最小值等于__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com