
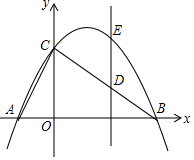
 ��ͼ��Rt��ABC���������������ƽ��ֱ������ϵ���������ϣ�OA=1��OB=4OA����ACB=90�㣬������y=ax2+bx+c��a��0����A��B��C���㣮
��ͼ��Rt��ABC���������������ƽ��ֱ������ϵ���������ϣ�OA=1��OB=4OA����ACB=90�㣬������y=ax2+bx+c��a��0����A��B��C���㣮���� ��1���������������A��B�����꣬�ɡ�AOC�ס�COB�������OC�ij��������ô���ϵ��������������ߵĺ�����ϵʽ��
��2����B��C��������ֱ��BC�Ľ���ʽ��������D�����꣬�Ӷ��ɱ�ʾ��DE�ij��������ö��κ��������ʿ���������ֵ��
��3������D�������Ϊt�������t�ֱ��ʾ��CE��CD��DE�ij�����CE=CD��CE=DE��CD=DE����������ֱ�õ�����t�ķ��̣������D������꣮
��� �⣺
��1����OA=1��OB=4OA��
��OB=4��
�ߡ�ACB=��AOB=��BOC=90�㣬
���ACO+��BCO=��BCO+��CBO=90�㣬
���ACO=��CBO��
���AOC�ס�COB��
��$\frac{AO}{OC}$=$\frac{OC}{OB}$����$\frac{1}{OC}$=$\frac{OC}{4}$�����OC=2��
��A��-1��0����B��4��0����C��0��2����
����������߽���ʽΪy=ax2+bx+2��
��A��B�����������ɵ�$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����B��4��0����C��0��2����
�����ֱ��BC����ʽΪy=kx+2��
��B���������ɵ�4k+2=0�����k=-$\frac{1}{2}$��
��ֱ��BC����ʽΪy=-$\frac{1}{2}$x+2��
�ߵ�D���߶�BC��һ���㣨����B��C�����غϣ���
�����D��x��-$\frac{1}{2}$x+2����0��x��4������E��x��-$\frac{1}{2}$x2+$\frac{3}{2}$x+2����
��DE��x�ᣬ
��DE=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2-��-$\frac{1}{2}$x+2��=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$��x-2��2+2��
��m=-$\frac{1}{2}$��x-2��2+2��
��-$\frac{1}{2}$��0��
�൱x=2ʱ��m�����ֵ2��
��3����D��t��-$\frac{1}{2}$t+2����0��t��4������E��t��-$\frac{1}{2}$t2+$\frac{3}{2}$t+2������C��0��2����
��CE=$\sqrt{{t}^{2}+��-\frac{1}{2}{t}^{2}+\frac{3}{2}t��^{2}}$��CD=$\sqrt{{t}^{2}+��-\frac{1}{2}t��^{2}}$=$\frac{\sqrt{5}}{2}$t��DE=-$\frac{1}{2}$t2+2t��
�ߡ�CDEΪ���������Σ�
����CE=CD��CE=DE��CD=DE���������
�ٵ�CE=CDʱ������$\sqrt{{t}^{2}+��-\frac{1}{2}{t}^{2}+\frac{3}{2}t��^{2}}$=$\frac{\sqrt{5}}{2}$t�����t=0����ȥ����t=2��
�ڵ�CE=DEʱ������$\sqrt{{t}^{2}+��-\frac{1}{2}{t}^{2}+\frac{3}{2}t��^{2}}$=-$\frac{1}{2}$t2+2t�����t=0����ȥ����t=$\frac{3}{2}$��
�۵�CD=DEʱ������$\frac{\sqrt{5}}{2}$t=-$\frac{1}{2}$t2+2t�����t=0����ȥ����t=4-$\sqrt{5}$��
���Ͽ�֪D��ĺ�����Ϊ2��$\frac{3}{2}$��4-$\sqrt{5}$��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ���������������ε��ж������ʡ����κ��������ʡ����ɶ��������������ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1�������A��B��C�������ǽ���Ĺؼ����ڣ�2������D�������ʾ��m�ǽ���Ĺؼ����ڣ�3������D������ֱ��ʾ��CD��CE��DE�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x10�£�x4��x2��=x8 | B�� | ��xy��5�£�xy��3=xy2 | ||
| C�� | 2xn+2��xn+1=x2 | D�� | ��6x3-3x2+3x���£�3x��=2x2-x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
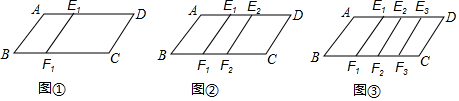
 ��ͼ��������ABCD�У�AD��BC��E��AB��һ�㣬EF��BC��CD�ڵ�F��AE��EB=1��2��AD=10��BC=25����EF�ij���
��ͼ��������ABCD�У�AD��BC��E��AB��һ�㣬EF��BC��CD�ڵ�F��AE��EB=1��2��AD=10��BC=25����EF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 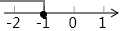 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com