
����Ŀ����ͼ�٣���һ��ֱ��������ֽƬ����B��90����AB��12��BC��8��С������м���һ���ԡ�BΪ�ڽ���������ľ��Σ������������֣���������λ��DE��EF����ʱ�����õľ��ε�������
��1����ͨ������˵��С���IJ����Ƿ���ȷ��
��2����ͼ�ڣ��ڡ�ABC�У�BC��10��BC���ϵĸ�AD��10������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵ��
��3����ͼ�ۣ��������ABCDE�У�AB��16��BC��20��AE��10��CD��8����A����B����C��90����С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
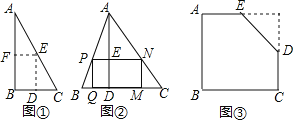
���𰸡���1����ȷ�����ɼ���������2����a��5ʱ��S����MNPQ���Ϊ25����3�����ε�������Ϊ180��
��������
(1)��BF=x����AF=12��x��֤����AFE�ס�ABC��������ʾ��EF�����������ʽ�ó�S����BDEF=��![]() (x��6)2+24�����ɵó����ۣ�
(x��6)2+24�����ɵó����ۣ�
(2)��DE=a��AE=10��a����֤����APN�ס�ABC�������ó�PN=10��a�����������ʽS����MNPQ=��(a��5)2+25�����ɵó������
(3)�ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K������IK������K��KL��BC��L���ɾ�������֪AE=EH=10��CD=DH=8���ֱ�֤��AEF�ա�HED����CDG�ա�HDE��AF=DH=8��CG=HE=10���Ӷ��жϳ���λ��IK�����˵����߶�AB��DE�ϣ�����(1)�Ľ��۽�ɣ�
(1)��ȷ�����ɣ�
��BF=x(0��x��12)��
��AB=12��
��AF=12��x��
����F��FE��BC��AC��E������E��ED��AB��BC��D��
���ı���BDEF��ƽ���ı��Σ�
�ߡ�B=90����
��BDEF�Ǿ��Σ�
��EF��BC��
���AFE�ס�ABC��
��![]() =
=![]() ��
��
��![]() ��
��
��EF=![]() (12��x)��
(12��x)��
��S����BDEF=EFBF=![]() (12��x)x=��
(12��x)x=��![]() (x��6)2+24
(x��6)2+24
�൱x=6ʱ��S����BDEF���=24��
��BF=6��AF=6��
��AF=BF��
�൱������λ��DE��EF����ʱ�����õľ��ε�������
(2)��DE=a��(0��a��10)��
��AD=10��
��AE=10��a��
���ı���MNPQ�Ǿ��Σ�
��PQ=DE=a��PN��BC��
���APN�ס�ABC��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��PN=10��a��
��S����MNPQ=PNPQ=(10��a)a=��(a��5)2+25��
�൱a=5ʱ��S����MNPQ���Ϊ25��
(3)�ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K������IK������K��KL��BC��L����ͼ����ʾ��
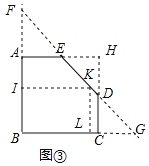
�ߡ�A=��HAB=��BCH=90����
���ı���ABCH�Ǿ��Σ�
��AB=16��BC=20��AE=10��CD=8��
��EH=10��DH=8��
��AE=EH��CD=DH��
�ڡ�AEF�͡�HED�У�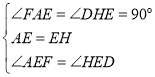 ��
��
���AEF�ա�HED(ASA)��
��AF=DH=8��
��BF=AB+AF=16+8=24��
ͬ����CDG�ա�HDE��
��CG=HE=10��
��BG=BC+CG=20+10=30��
��BI=![]() BF=12��
BF=12��
��BI=12��16��
����λ��IK�����˵����߶�AB��DE�ϣ�
��IK=![]() BG=15��
BG=15��
��(1)֪���ε�������ΪBIIK=12��15=180��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ�
����һ��˳�������ŵ�һ������Ϊ���У������е�ÿһ��������������е�����ڵ�һλ������Ϊ��һ���Ϊ![]() �����ڵڶ�λ������Ϊ�ڶ����Ϊ
�����ڵڶ�λ������Ϊ�ڶ����Ϊ![]() ���������ƣ����ڵ�nλ������Ϊ��n���Ϊ
���������ƣ����ڵ�nλ������Ϊ��n���Ϊ![]() �����ԣ����е�һ����ʽ����д�ɣ�
�����ԣ����е�һ����ʽ����д�ɣ�![]() ��
��![]() ��
��![]() ������
������![]() ��
��
һ��أ����һ�����дӵڶ�����ÿһ������ǰһ��IJ����ͬһ����������ô������н����Ȳ����У�������������Ȳ����еĹ������ͨ����d��ʾ���磺����1��3��5��7����Ϊ�Ȳ����У�����![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
�������ϲ��ϣ�����������⣺
(1)�Ȳ�����5��10��15�����Ĺ���dΪ______����5����______��
(2)���һ������![]() ��
��![]() ��
��![]() ������
������![]() �����ǵȲ����У��ҹ���Ϊd����ô���ݶ���ɵõ���
�����ǵȲ����У��ҹ���Ϊd����ô���ݶ���ɵõ���![]() ��
��![]() ��
��![]() ������
������![]() ������
������
����![]() ��
��
![]() ��
��
![]() ��
��
������
�ɴˣ����������ɵȲ����е�ͨ�ʽ��![]() (______)d��
(______)d��
(3)![]() �Dz��ǵȲ�����
�Dz��ǵȲ�����![]() ��
��![]() ��
��![]() ���������ǣ��ǵڼ��
���������ǣ��ǵڼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���A=36����AB=AC��BDƽ�֡�ABC����ͼ�е��������εĸ����ǣ� ��
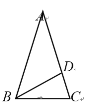
A.0��B.1��C.2��D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB����O��ֱ����AC���ң�ֱ��EF������C��AD��EF�ڵ�D����DAC=��BAC��
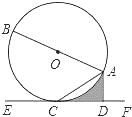
��1����֤��EF����O�����ߣ�
��2������O�İ뾶Ϊ2����ACD=30������ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y����![]() ��x+1����x��9���������ύ��A��B��C���㣬DΪ���㣬����AC��BC����P�Ǹ��������ڵ�һ�������ϵ�һ�㣮����P��y���ƽ���߽�BC�ڵ�E������AP��BC�ڵ�F����
��x+1����x��9���������ύ��A��B��C���㣬DΪ���㣬����AC��BC����P�Ǹ��������ڵ�һ�������ϵ�һ�㣮����P��y���ƽ���߽�BC�ڵ�E������AP��BC�ڵ�F����![]() �����ֵΪ_______��
�����ֵΪ_______��
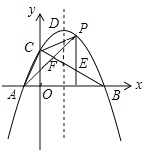
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵����� A��B ����Ʒ�ƵIJ�ɫ���ӻ���A��B ���ֲʵ�Ľ���ÿ̨�ֱ�Ϊ2000 Ԫ��1600Ԫ��һ �� �� A��B �� �� �� �� ÿ ̨ �� �� �� �� �� Ϊ 2700 Ԫ��2100 Ԫ���� �� �� Ϊ 12000Ԫ��Ϊ�����������·�Ӫ����Ա�ṩ���������۲��ԣ�
����һ�� A �ֲʵ�ÿ̨����100Ԫ��B �ֲʵ�ÿ̨����80Ԫ���������������ֱ�����30%��40%��
���Զ��� A �ֲʵ�ÿ̨���� 150 Ԫ��B �ֲʵ�ÿ̨���� 100 Ԫ��������������������50%��
����������Ϣ������и��⣺
��1����һ�·� A��B ���ֲʵ����������
��2�����·������ֲ����Ƿ�����������
��3�����·ݸ��̵�Ӧ�ò��������������۲����е���һ�֣�����ʹ�̵�����õ�����϶ࣿ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �������ύ��
�������ύ��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ��ࣩ����
��ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��
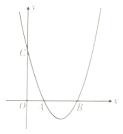
��1������ֱ�ߺ�Բ�棬����������![]() �ĶԳ��ᣨ�߹���ͼ��������ͼ�ۼ�����д��������
�ĶԳ��ᣨ�߹���ͼ��������ͼ�ۼ�����д��������
��2����![]() �ǵ���ֱ�������Σ���������Ϊ3����
�ǵ���ֱ�������Σ���������Ϊ3����![]() ��ֵ��
��ֵ��
��3���ڣ�2���������£���![]() Ϊ�����߶Գ����ϵ�һ�㣬��
Ϊ�����߶Գ����ϵ�һ�㣬��![]() ����СֵΪ________��
����СֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻͬѧ�ǵĿ������ijѧУ������������Ȼ���������������ȡ�˲���ѧ����������Ϊ��������ȥ�ľ����ǣ������ʾ����飬Ҫ��ѧ��ֻ�ܴ���![]() ��ֲ������
��ֲ������![]() ����������
����������![]() ��ʪ�ع�����
��ʪ�ع�����![]() ����´ɽ�����ĸ�������ѡ��һ�������ݵ�������������������������ͳ��ͼ��
����´ɽ�����ĸ�������ѡ��һ�������ݵ�������������������������ͳ��ͼ��
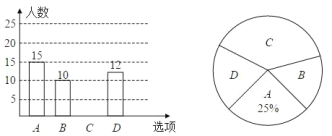
��1������ʾ������������_________�ˣ�
��2����ȫ����ͳ��ͼ��
��3��������![]() ���������ε�Բ�ĽǶ���Ϊ_________��
���������ε�Բ�ĽǶ���Ϊ_________��
��4������ѧУ����3000��ѧ��������Ƹ�У����ȥ��´ɽ��ѧ��ԼΪ_________�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�ꡰ519����Ҫ�ߣ�ȫ��ͽ���գ�����վ�������������������ġ�ͽ�����5��19���������Ļ�ɽ���½��ؾ���.��ί�ᣨ����췽��Ϊ�˽������ȡ���˺óɼ��IJ���ѡ�֣��ƻ�����100���ļס������ּ���Ʒ����.���м��ּ���Ʒÿ���ۼ�120Ԫ�����ּ���Ʒÿ���ۼ�80Ԫ.
��1���������ס������ּ���Ʒһ��������9600Ԫ������ס������ּ���Ʒ���Ƕ��ټ���
��2���蹺����ּ���Ʒ![]() ��������������ּ���Ʒ�ļ������������ּ���Ʒ��������2���������ܷ��ò�����9400Ԫ.����ί�Ṻ��ס������ּ���Ʒ���м��ַ�������һ�ַ��������ܷ������٣������ܷ����Ƕ���Ԫ��
��������������ּ���Ʒ�ļ������������ּ���Ʒ��������2���������ܷ��ò�����9400Ԫ.����ί�Ṻ��ס������ּ���Ʒ���м��ַ�������һ�ַ��������ܷ������٣������ܷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com