练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．有一个长方体水箱，从水箱里面量得它的深是30cm，底面的长是25cm，宽是20cm．水箱里盛有深为acm（0＜a≤8）的水，若往水箱里放入棱长为10cm的立方体铁块，则此时水深为$\frac{5}{4}$a．

    分析 先求出水箱的容量，然后根据题意，求出水深为acm时水的体积、棱长为10cm立方体铁块的体积．根据条件从而求出此时的水深．

    解答 解：水箱的容量为30×25×20=15000
    水深为acm时，水的体积为a×25×20=500a
    棱长为10cm立方体铁块的体积为10×10×10=1000
    当铁块放入水箱时，
    ∵0＜a≤8，铁块并未完全落入水中，
    设此时水深为x，则10×10×x+500a=25×20×x
    所以此时x=$\frac{5}{4}$a，
    故答案为：$\frac{5}{4}$a．

    点评 本题主要考查列代数式的能力，解题关键是要读懂题目的意思，根据题目给出的条件，列出式子从而求解，同时还有物理知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．如图，在△ABC中，∠C=90°，点O为AB上一点，以O为圆心，OA为半径的圆与BC相切于点D．求证：AD平分∠CAB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，∠1=70°，∠2=110°，∠C=∠D，试探索∠A与∠F有怎样的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，点P是Rt△ABC斜边AB上的一点，PE⊥AC于点E，PF⊥BC于点F，BC=5，AC=12，求线段EF长度的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如果关于x的一元二次方程ax2+bx+c=0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，研究发现了此类方程的一般性结论：设其中一根为t，则另一个根为2t，因此ax2+bx+c=a（x-t）（x-2t）=ax2-3atx+2t2a，所以有b2-$\frac{9}{2}$ac=0；我们记“K=b2-$\frac{9}{2}$ac”即K=0时，方程ax2+bx+c=0为倍根方程；下面我们根据此结论来解决问题：
    （1）方程①x2-x-2=0；方程②x2-6x+8=0这两个方程中，是倍根方程的是②（填序号即可）；
    （2）若（x-2）（mx+n）=0是倍根方程，求4m2+5mn+n2的值；
    （3）关于x的一元二次方程x2-$\sqrt{m}x+\frac{2}{3}$n=0（m≥0）是倍根方程，且点A（m，n）在一次函数y=3x-8的图象上，求此倍根方程的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

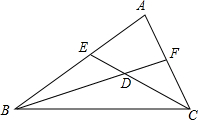    1．如图，在△ABC中，BF与CE交于点D，若BF和CE分别平分∠ABC和∠ACB．
    （1）已知∠A=40°，求∠BDC的度数．
    （2）已知∠BDC=130°，求∠A的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，已知AB=AC，∠BAC=∠DAE，∠ABD=∠ACE，问BD与CE相等吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．规定x*y=-|y|，x△y=-x，如当x=3，y=4时，x*y=-|4|=-4，x△y=-3，根据以上运算法则比较5*（-7）与5△（-7）的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知x=$\frac{（-1）^{n-1}-（-1）^{n}}{2}$，（n为整数），求：x-2x2+3x3-4x4+…+99x99-100x100的值．

    查看答案和解析>>

    同步练习册答案