
【题目】如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.
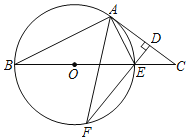
(1)求证:AC为⊙O切线.
(2)若AB=5,DF=4,求⊙O半径长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连结OA,根据已知条件得到∠AOE=∠BEF,根据平行线的性质得到OA⊥AC,于是得到结论;
(2)连接OF,设∠AFE=α,则∠BEF=2α,得到∠BAF=∠BEF=2α,得到∠OAF=∠BAO=α,求得∠AFO=∠OAF=α,根据全等三角形的性质得到AB=AF=5,由勾股定理得到AD=![]() =3,根据圆周角定理得到∠BAE=90°,根据相似三角形的性质即可得到结论.
=3,根据圆周角定理得到∠BAE=90°,根据相似三角形的性质即可得到结论.
解(1)证明:连结OA,
∴∠AOE=2∠F,
∵∠BEF=2∠F,
∴∠AOE=∠BEF,
∴AO∥DF,
∵DF⊥AC,
∴OA⊥AC,
∴AC为⊙O切线;
(2)解:连接OF,
∵∠BEF=2∠F,
∴设∠AFE=α,则∠BEF=2α,
∴∠BAF=∠BEF=2α,
∵∠B=∠AFE=α,
∴∠BAO=∠B=α,
∴∠OAF=∠BAO=α,
∵OA=OF,
∴∠AFO=∠OAF=α,
∴△ABO≌△AFO(AAS),
∴AB=AF=5,
∵DF=4,
∴AD=![]() =3,
=3,
∵BE是⊙O的直径,
∴∠BAE=90°,
∴∠BAE=∠FDA,
∵∠B=∠AFD,
∴△ABE∽△DFA,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BE=![]() ,
,
∴⊙O半径=![]() .
.


科目:初中数学 来源: 题型:
【题目】赵化鑫城某超市购进了一批单价为16元的日用品,销售一段时间后,为获得更多的利润,商场决定提高销售的价格,经试验发现,若按每件20元销售,每月能卖360件;若按每件25元销售,每月能卖210件;若每月的销售件数y(件)与价格x(元/件)满足y=kx+b.
(1)求出k与b的值,并指出x的取值范围?
(2)为了使每月获得价格利润1920元,商品价格应定为多少元?
(3)要使每月利润最大,商品价格又应定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,路灯下,广告标杆AB的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一棵树,它的影子是MN.
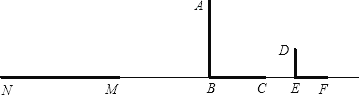
(1)请在图中画出表示树高的线段.(不写作法,保留作图痕迹)
(2)若已知点N、F到路灯的底部距离相等,小明身高1.6米,影长EF为1.8米,树的影长MN是6米,请计算树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
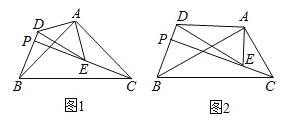
(1)问题提出:如图1,若![]() ,
,![]() .
.
①![]() 与
与![]() 的数量关系为________;
的数量关系为________;
②![]() 的度数为________.
的度数为________.
(2)猜想论证:如图2,若![]() ,则(1)中的结论是否成立?请说明理由.
,则(1)中的结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
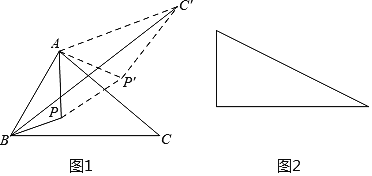
【题目】问题的提出:
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
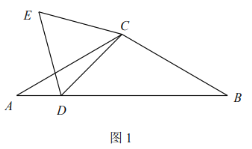
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() .
.
![]() 如图1,若
如图1,若![]() 求等边
求等边![]() 的边长;
的边长;
![]() 如图2,点
如图2,点![]() 在
在![]() 边上移动过程中,连接
边上移动过程中,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
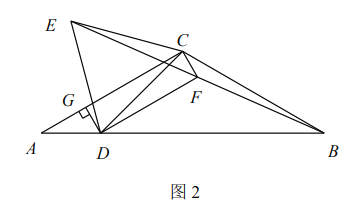
①求证:![]() ;
;
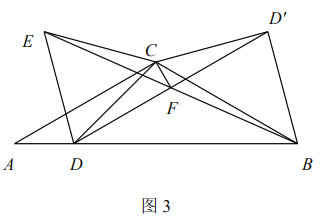
②如图3,将![]() 沿
沿![]() 翻折得
翻折得![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() .则下列结论:①
.则下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的中点.其中正确的是( )
的中点.其中正确的是( )
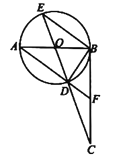
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的长.
.求BD的长.
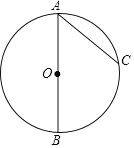
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com