
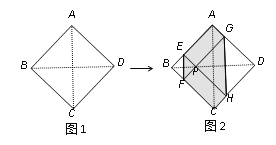
【题目】如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:①当x=1时,点P是正方形ABCD的中心;②当x=![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是3;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确的选项是( )
A. ①③ B. ①②④ C. ①③④ D. ①②③④
【答案】C
【解析】(1)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF和△DGH是等腰直角三角形,∴当AE=1时,重合点P是BD的中点,∴点P是正方形ABCD的中心;故①结论正确;
(2)正方形纸片ABCD,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,∴△BEF∽△BAC,∵x=![]() ,∴BE=2﹣
,∴BE=2﹣![]() =
=![]() ,∴
,∴![]() ,即
,即![]() ,∴EF=
,∴EF=![]() AC,同理,GH=
AC,同理,GH=![]() AC,∴EF+GH=AC,故②结论错误;
AC,∴EF+GH=AC,故②结论错误;
(3)六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积.∵AE=x,∴六边形AEFCHG面积=22﹣![]() BEBF﹣
BEBF﹣![]() GDHD=4﹣
GDHD=4﹣![]() ×(2﹣x)(2﹣x)﹣
×(2﹣x)(2﹣x)﹣![]() xx=﹣x2+2x+2=﹣(x﹣1)2+3,∴六边形AEFCHG面积的最大值是3,故③结论正确;
xx=﹣x2+2x+2=﹣(x﹣1)2+3,∴六边形AEFCHG面积的最大值是3,故③结论正确;
(4)当0<x<2时,∵EF+GH=AC,六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=(AE+CH)+(FC+AG)+(EF+GH)=2+2+2![]() =4+2
=4+2![]() 故六边形AEFCHG周长的值不变,故④结论正确.
故六边形AEFCHG周长的值不变,故④结论正确.
故选C.


科目:初中数学 来源: 题型:
【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元,一律按原价打九折;
③一次性购书超过200元,一律按原价打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚在课外书中看到这样一道有理数的混合运算题:
计算:![]()
她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,他顺利地解答了这道题。
(1)前后两部分之间存在着什么关系?
(2)先计算哪步分比较简便?并请计算比较简便的那部分。
(3)利用(1)中的关系,直接写出另一部分的结果。
(4)根据以上分析,求出原式的结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
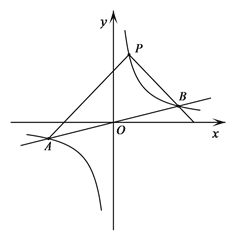
【题目】如图,反比例函数y=![]() 的图象与一次函数y=
的图象与一次函数y=![]() x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
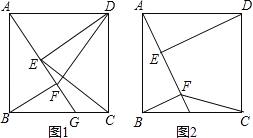
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB=![]() ,G为CB中点,连接CF,直接写出四边形CDEF的面积.
,G为CB中点,连接CF,直接写出四边形CDEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(a ,2![]() )是直线y=
)是直线y=![]() x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则
x上一点,以A为圆心,2为半径作⊙A,若P(x,y)是第一象限内⊙A上任意一点,则![]() 的最小值为( )
的最小值为( )
A. 1 B. ![]() C.
C. ![]() —1 D.
—1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
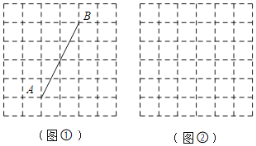
【题目】如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点.
(1)在图①中,线段AB的长度为 ;若在图中画出以C为直角顶点的Rt△ABC,使点C在格点上,请在图中画出所有点C;
(2)在图②中,以格点为顶点,请先用无刻度的直尺画正方形ABCD,使它的面积为13;再画一条直线PQ(不与正方形对角线重合),使PQ恰好将正方形ABCD的面积二等分(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
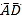
(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com