
【题目】如图,在长方形纸片![]() 中,
中,![]() ,折叠纸片,使得点
,折叠纸片,使得点![]() 落在
落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,点
,点![]() 分别在边
分别在边![]() 和
和![]() 上,当点
上,当点![]() 恰好是
恰好是![]() 边的中点时,点
边的中点时,点![]() 与点
与点![]() 重合,若在折叠过程中
重合,若在折叠过程中![]() ,则
,则![]() 等于________
等于________![]() .
.

【答案】9
【解析】
先求出BC的长,过点N作HN⊥CD,由勾股定理可求NB的长,由等腰三角形的性质可求PC的长,即可求PD的长.
如图1,当点P恰好是CD边的中点时,点N与点B重合,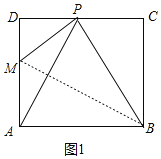
∵点P是CD的中点,
∴CP=![]() CD=6cm,
CD=6cm,
由折叠的性质可得:AB=PB=12cm,
∴BC=![]() ,
,
如图2,折叠过程中NP=NC,过点N作HN⊥CD,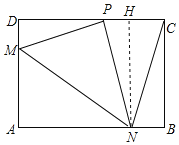
由折叠的性质可得:AN=PN=NC,
∵NB2+BC2=NC2,
∴NB2+108=(12-NB)2,
∴NB=![]() cm,
cm,
∵NH⊥CD,∠ABC=∠BCD=90°,
∴四边形BCHN是矩形,
∴HC=BN=![]() cm,
cm,
∵NC=NP,NH⊥CD,
∴PC=2HC=3cm,
∴PD=CD-PC=9cm,
故答案为:9cm.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】(阅读)如图1,等边△ABC中,P是AC边上一点,Q是CB延长线上一点,若AP=BQ.则过P作PF∥BC交AB于F,可证△APF是等边三角形,再证△PDF≌QDB可得D是FB的中点.请写出证明过程.
(运用)如图2,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A,C不重合),Q是CB延长线上一动点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.

(1)当∠BQD=30°时,求AP的长;
(2)在运动过程中线段ED的长是否发生变化?如果不变,直接写出线段ED的长;如果发生改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象 与x轴、y轴分别交于点A,B.
的图象 与x轴、y轴分别交于点A,B.

(1)求点A,B的坐标;
(2)M为ー次函数y=x+3的图象上一点,若 △ABM与△ABO的面积相等,求点M的坐标;
(3)Q为y轴上的一点,若三角形ABQ为等腰三角形 ,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AB的垂直平分线EF分別交AC、AB边于E、F点.若点O为BC边的中点,点M为线段EF上一动点,则△BOM周长的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:①∠AMD=90°;②M为BC的中点;③AB+CD=AD;④S△ADM=S梯形ABCD;⑤M到AD的距离等于BC的一半.其中正确的结论有____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从这个袋子中任意摸只球,组成一个两位数,求所组成的两位数是5的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,A点坐标为(4,3),B点坐标为(-1,4),C点坐标为(-3,1).
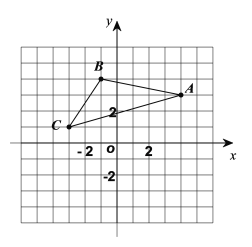
(1)在图中画出△ABC关于x轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.
(2)在x轴上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你观察下列式子:
![]()
![]()
![]()
![]()
……
根据上面的规律,解答下列问题:
(1)当![]() 时,
时,
计算![]() …
…![]() =_________;
=_________;
(2)设![]() …
…![]() ,则a的个位数字为 ;
,则a的个位数字为 ;
(3)求式子![]() …
…![]() 的和.
的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com