
分析 (1)首先把等号左边分解因式可得(x-4)(x+2)=0,进而可得x-4=0,x+2=0,再解即可;
(2)首先确定方程中a、b、c的值,然后计算出△,再用求根公式计算即可;
(3)首先把方程整理成一般式可得x2-10x+9=0,把等号左边分解因式可得(x-9)(x-1)=0,进而可得x-9=0,x-1=0,再解即可;
(4)首先去分母,把方程整理成一般式可得x2+x-6=0,把等号左边分解因式可得(x+3)(x-2)=0,进而可得x+3=0,x-2=0,再解即可.
解答 解:(1)x2-2x-8=0,
(x-4)(x+2)=0,
则x-4=0,x+2=0,
解得:x1=4,x2=-2;
(2)a=2,b=-5,c=-2,
△=b2-4ac=25+16=41,
x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{5±\sqrt{41}}{4}$,
则${x_1}=\frac{{5+\sqrt{41}}}{4},{x_2}=\frac{{5-\sqrt{41}}}{4}$;
(3)(x-3)2=12+4(x-3),
x2-6x+9-12-4x+12=0,
x2-10x+9=0,
(x-9)(x-1)=0,
则x-9=0,x-1=0,
解得:x1=9,x2=1;
(4)2(x+1)-3(x-1)=(x+1)(x-1),
2x+2-3x+3=x2-1,
x2+x-6=0,
(x+3)(x-2)=0.
x+3=0,x-2=0,
解得:x1=-3,x2=2,
检验:当x=-3时,(x+1)(x-1)≠0,
当x=2时,(x+1)(x-1)≠0,
所以:方程的解集为x1=-3,x2=2.
点评 此题主要考查了一元二次方程的解法,关键是掌握因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:填空题
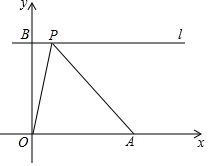 如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.
如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
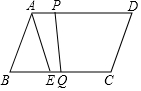 如图,四边形ABCD为平行四边形,在BC上取一点E,连接AE,∠ABC=∠DAE.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为13cm/s,沿A-D-A运动时的速度为8cm/s.点Q从点B出发沿BC方向运动,运动速度为5cm/s,P,Q两点同时从点B出发,当点Q到达点C时,P,Q两点同时停止运动.设点P的运动时间为t(s),连接PQ,已知AB=26cm,BC=40cm,点A到边BC的距离为24cm.
如图,四边形ABCD为平行四边形,在BC上取一点E,连接AE,∠ABC=∠DAE.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为13cm/s,沿A-D-A运动时的速度为8cm/s.点Q从点B出发沿BC方向运动,运动速度为5cm/s,P,Q两点同时从点B出发,当点Q到达点C时,P,Q两点同时停止运动.设点P的运动时间为t(s),连接PQ,已知AB=26cm,BC=40cm,点A到边BC的距离为24cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com