练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．关于x的不等式x-3＞$\frac{3x+a}{2}$的解集在数轴上表示如图所示，则a的值是-12．

    分析 先把a当作已知条件表示出x的取值范围，再与数轴上已知x的取值范围相比较即可得出a的值．

    解答 解：解不等式x-3＞$\frac{3x+a}{2}$得，x＜-6-a．
    ∵由数轴上不等式的解集可知x＜6，
    ∴-6-a=6，解得a=-12．
    故答案为：-12．

    点评 本题考查的是在数轴上表示不等式的解集，熟知“小于向左，大于向右”是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

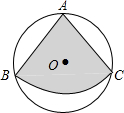    17．如图，从一个直径为4的圆形铁皮中剪下一个圆心角为60°的扇形ABC，将剪下来的扇形围成一个圆锥，则圆锥的底面圆半径为（　　）
    A．$\frac{2}{3}$B．$\frac{{\sqrt{3}}}{3}$C．$\frac{{2\sqrt{3}}}{3}$D．$\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列事件中，概率不是$\frac{1}{3}$的事件是（　　）
    A．向空中抛2枚同样的一元硬币，如果落地后一正一反
    B．在“石头、剪刀、布”的游戏中，小明随机出“剪刀”
    C．暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是红球
    D．掷一个质地均匀的正六面体骰子，向上的面点数是大于4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，在Rt△ABC中，∠ABC=90°，AB=8，BC=4，DE垂直平分斜边AC，交AB于D，E为垂足，连接CD，则AD的长为（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．某兴趣小组用高为1.2米的仪器测量建筑物CD的高度．如示意图，由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为β，在A和C之间选一点B，由B处用仪器观察建筑物顶部D的仰角为α．测得A，B之间的距离为4米，tanα=1.6，tanβ=1.2，试求建筑物CD的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

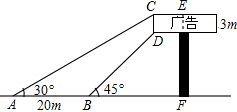    12．如图，某广告牌竖直矗立在水平地面上，经测量得到如下相关数据：CD=3m，AB=20m，∠CAB=30°，∠DBF=45°，求广告牌的高EF（结果保留根号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

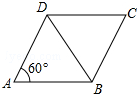    19．如图，已知菱形ABCD的边长为2，∠DAB=60°，则对角线AC的长是（　　）
    A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．当多项式-5x2-（2m-1）x2+（2-3n）x-1不含二次项和一次项时，则m=-2；n=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

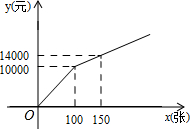    17．在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）．现有两种购买方案：
    方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张50元；（总费用=广告赞助费+门票费）
    方案二：购买门票方式如图所示．
    解答下列问题：
    （1）方案一中，y与x的函数关系式为y=50x+10000；方案二中，当0≤x≤100时，y与x的函数关系式为y=100x，当x＞100时，y与x的函数关系式为y=80x+2000；
    （2）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共600张，花去总费用计48000元，求甲、乙两单位各购买门票多少张．

    查看答案和解析>>

    同步练习册答案