
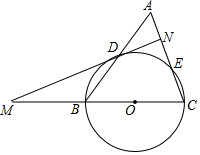
 如图,△ABC中,AC=BC=a,AB=b,以BC为直径作⊙O交AB于点D,交AC于点E,过点D作⊙O的切线MN,交CB的延长线于点M,交AC于点N.
如图,△ABC中,AC=BC=a,AB=b,以BC为直径作⊙O交AB于点D,交AC于点E,过点D作⊙O的切线MN,交CB的延长线于点M,交AC于点N.分析 (1)连接OD、CD,由BC是直径可知∠BDC=90°,易证OD是△ABC的中位线,从而可知OD∥AC,由切线的性质可知:∠MDO=90°=∠MNC,从而得证.
(2)由于∠BEC=90°,AD与AC的长度已知,利用勾股定理即可求出CD的长度,然后利用等面积即可求出BE的长度.
解答 解:(1)连接 OD,CD.
∵BC 是⊙O 的直径,
∴∠BDC=90°,即CD⊥AB
∵AC=BC,∴D是AB的中点
又∵BC 是⊙O 的直径,即O 为 BC的中点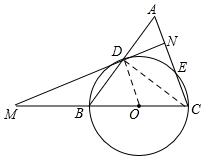
∴OD∥AC,∠MDO=∠MNC
∵MN是⊙O 的切线,切点为D
∴OD⊥MN,即∠MDO=90°=∠MNC
∴MN⊥AC
(2)由BC 是⊙O 的直径,可得∠BEC=90°;
由CD⊥AB,在 Rt△ACD 中,AD、AC的长可知,
用勾股定理可求CD的长;
由AB?CD=2S△ABC=AC?BE,可得BE的长.
点评 本题考查圆的综合问题,涉及切线的性质,等腰三角形的性质,中位线的性质,勾股定理等知识,综合程度较高,属于中等题型.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
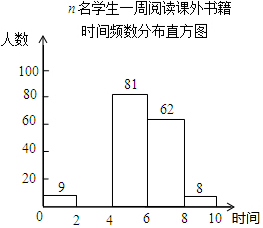 某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.| 时间段 | 频数 |
| 0<t≤2 | 9 |
| 2<t≤4 | 40 |
| 4<t≤6 | 81 |
| 6<t≤8 | 62 |
| 8<t≤10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
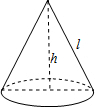 如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )| A. | 60π | B. | 65π | C. | 78π | D. | 156π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com