
分析 根据x的取值范围,利用绝对值的性质去掉绝对值号依次讨论求解即可.
解答 解:当x≥5时,a=x-1-2(x-2)+2(x-3)-(x-5)=2,
此时,方程有无数解,
当3≤x<5时,a=x-1-2(x-2)+2(x-3)-(5-x)=2x-8,
所以,3≤$\frac{8+a}{2}$<5,
解得-2≤a<2,
当2≤x<3时,a=x-1-2(x-2)+2(3-x)-(5-x)=-2x+4,
所以,2≤$\frac{4-a}{2}$<3,
解得-2<a≤0,
当1≤x<2时,a=x-1-2(2-x)+2(3-x)-(5-x)=2x-4,
所以,1≤$\frac{a+4}{2}$<2,
解得-2≤a≤0,
x<1时,a=1-x-2(2-x)+2(3-x)-(5-x)=-4,
此时,方程有无数解,
综上所述,-2≤a<2时,方程有唯一解.
点评 本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:填空题
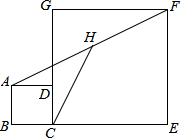 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=4,H是AF的中点,那么CH的长是$\frac{1}{2}\sqrt{34}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法:
甲、乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走,设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象如图所示,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π)
如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
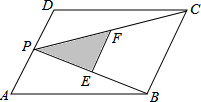 如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值:
如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值:| A. | ②③ | B. | ②⑤ | C. | ④⑤ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com