
【题目】如图,在平面直角坐标系中,顶点为(2,﹣1)的抛物线交y轴于A点,交x轴于B、C两点(点B在点C的左侧),已知A点坐标为(0,3),连接AB.
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
【答案】
(1)解:设抛物线的解析式为y=a(x﹣2)2﹣1
把A(0,3)代入得:3=4a﹣1
解得:a=1,
故 y=(x﹣2)2﹣1
=x2﹣4x+3
(2)解:抛物线的对称轴与⊙C相离
理由如下:
如图1,过点C作CE⊥BD于E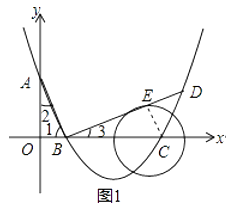
令y=0,则x2﹣4x+3=0
解得:x1=1,x2=3
则B(1,0),C(3,0),A(0,3),
故AB= ![]() ,
,
∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∴△AOB~△BEC
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CE= ![]()
![]() ,
,
∴BF=CE=1> ![]()
![]() ,
,
∴抛物线的对称轴与⊙C相离
(3)解:设P(m,m2﹣4m+3),如图2,过点P作作PQ∥y轴交AC于点Q,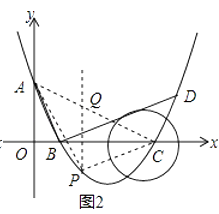
设AC的解析式为:y=kx+b,
故 ![]() ,
,
解得: ![]() ,
,
故AC的解析式为:y=﹣x+3,
则Q(m,﹣m+3),
则PQ=﹣m+3﹣(m2﹣4m+3)=﹣m2+3m,
S△PAC=S△AQP+S△CQP
= ![]() ×3(﹣m2+3m),
×3(﹣m2+3m),
=﹣ ![]() m2+
m2+ ![]() m,
m,
则m=﹣ ![]() =
= ![]() ÷3=
÷3= ![]() ,
,
把m= ![]() 代入得:﹣
代入得:﹣ ![]() ×
× ![]() +
+ ![]() ×
× ![]() =
= ![]() ,
,
故p( ![]() ,﹣
,﹣ ![]() ),
),
则S△PAC的最大值= ![]() .
.
【解析】(1)可设抛物线为顶点式,再把(0,3)代入即可;(2)判定直线和圆的位置关系需比较“d与r的大小”,通过相似,即△AOB~△BEC,求出圆的半径CE,圆心到直线的距离CF=d=1;(3)最值问题可利用函数思想,构建以P的横坐标x为自变量、S△PAC为因变量的函数,配方法求出最值.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】4月21日是重庆一中校庆日,学校每一年都要举行校庆活动和教职工运动会,全校分校区或年级组队进行角逐,今年某校区给参赛老师购买了![]() 、
、![]() 、
、![]() 三种运动服,每一套价格分别是400元,500元,600元,其中
三种运动服,每一套价格分别是400元,500元,600元,其中![]() 种运动服套数是
种运动服套数是![]() 种运动服套数的3倍,
种运动服套数的3倍,![]() 种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
种运动服套数比C种运动服套数的2倍还多,要求购买服装的总套数尽量多且总费用不超过52300元,则能购买到运动服最多_________套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从-2,-1,0,1,2,3,5这七个数中,随机抽取一个数记为m,若数m使关于x的不等式组![]() 无解,且使关于x的一元一次方程(m-2)x=3有整数解,那么这六个数所有满足条件的m的个数有( )
无解,且使关于x的一元一次方程(m-2)x=3有整数解,那么这六个数所有满足条件的m的个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为10,在⊙O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CP的垂线CD交PB的延长线于D点.
(1)求证:ACCD=PCBC;
(2)当点P运动到AB弧中点时,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 、
、![]() 是直线,
是直线,![]() ,
,![]() ,
,![]() .
.![]() 与
与![]() 平行吗?为什么?
平行吗?为什么?

解:![]() ,理由如下:
,理由如下:
∵![]() (已知)
(已知)
∴![]() ( )
( )
∵![]() (已知)
(已知)
∴![]() _________( )
_________( )
∵![]() (已知)
(已知)
∴![]() ( )
( )
即![]()
∴![]() _________(等量代换)
_________(等量代换)
∴![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com