
【题目】如图1,在△ABC中,∠C=90°,延长CA至点D,使AD=AB.设F为线段AB上一点,连接DF,以DF为斜边作等腰Rt△DEF,且使AE⊥AB.
(1)求证:AE=AF+BC;
(2)当点F为BA延长线上一点,而其余条件保持不变,如图2所示,试探究AE、AF、BC之间的数量关系,并说明理由.

【答案】(1)见解析;(2)AE+AF=BC.理由见解析
【解析】
(1)过D作DM⊥AE于M,在△DEM中,由余角的定义得到∠DEM+∠EDM=90°,由于∠DEM+∠AEF=90°,推出∠AEF=∠EDM证得△DEM≌△EFA,根据全等三角形的性质得到AF=EM,根据三角形的内角和和余角的定义得到∠EAD=∠B,推出△DAM≌△ABC,根据全等三角形的性质得到BC=AM即可得到结论;
(2)如图2,过D作DM⊥AE交AE的延长线于M,根据余角的定义和三角形的内角和得到∠EAD=∠B,证得△ADM≌△BAC,由全等三角形的性质得到BC=AM,由于EF=DE,∠DEF=90°,推出∠AEF=∠MDE,证得△MED≌△AFE,根据全等三角形的性质得到ME=AF,即可得到结论.
(1)证明:如图1,过D作DM⊥AE于M,在△DEM中,∠DEM+∠EDM=90°,

∵∠DEM+∠AEF=90°,
∴∠AEF=∠EDM,
∵DE=FE,
在△DEM与△EFA中,
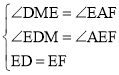 ,
,
∴△DEM≌△EFA(AAS),
∴AF=EM,
∵∠BAC+∠B=90°,
∵∠EAD+∠EAB+∠BAC=180°,
∴∠EAD+∠BAC=90°,
∴∠EAD=∠B,
在△DAM与△ABC中,
 ,
,
∴△DAM≌△ABC(AAS),
∴BC=AM,
∴AE=EM+AM=AF+BC;
(2)解:AE+AF=BC.理由如下:
如图2,过D作DM⊥AE交AE的延长线于M,
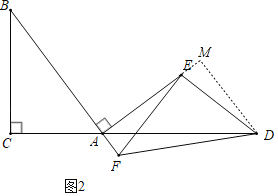
∵∠C=90°,
∴∠BAC+∠B=90°,
∵∠EAD+∠MAB+∠BAC=180°,∠MAB=90°,
∴∠EAD+∠BAC=90°,∠EAD=∠B,
在△ADM与△BAC中,
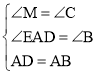 ,
,
∴△ADM≌△BAC(AAS),
∴BC=AM,
∵EF=DE,∠DEF=90°,
∵∠MED+∠DEF+∠AEF=180°,
∴∠MED+∠AEF=90°,
∵∠MED+∠MDE=90°,
∴∠AEF=∠MDE,
在△MED与△AFE中,
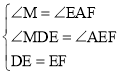 ,
,
∴△MED≌△AFE(AAS),
∴ME=AF,
∴AE+AF=AE+ME=AM=BC,
即AE+AF=BC.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数
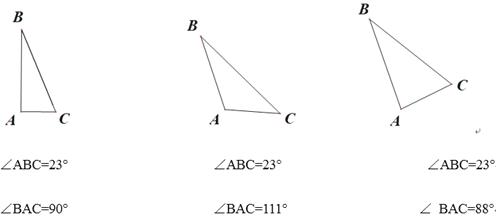
(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.
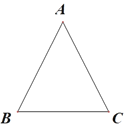
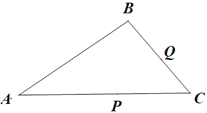
(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=50cm,BC=30cm,AC=40cm.

(1)求证:∠ACB=90°
(2)求AB边上的高.
(3)点D从点B出发在线段AB上以2cm/s的速度向终点A运动,设点D的运动时间为t(s).
①BD的长用含t的代数式表示为 .
②当△BCD为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求:汽车行驶中每千米用电费用是多少元?甲、乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过50元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC=65°,D为∠BAC内部一点,过D作DB⊥AB于B,DC⊥AC于C,设点E、点F分别为AB、AC上的动点,当△DEF的周长最小时,∠EDF的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是 ;
(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“基善一日捐册”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
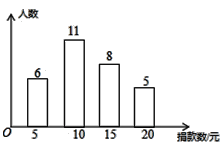
(1)本次调查中,一共调查了________名同学;
(2)抽查学生捐款数额的众数是_______元,中位数是_______元;
(3)该校共有600名学生参与捐款,请你估计该校学生捐款不少于15元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,过点B作BD⊥AC,垂足为D,若D是边AC的中点,
(1)求证:△ABC是等边三角形;
(2)在线段BD上求作点E,使得CE=2DE(要求:尺规作图,不写画法,保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上我们可以发现其中某些数满足一定的规律.如图是2018年8月份的日历,我们任意选择其中所示的方框部分,将方框部分中的4个位置的数交叉相乘,再相减,如8×16-9×15=-7,19×27-20×26=-7,不难发现结果都是-7.
(1)请你再选择一组数按上面的方式计算,看看是否符合这个规律.并用你擅长的表达方式描述这个规律.
(2)请你利用整式的运算对以上的规律加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com